题目内容
 甲、乙两车都从同一地点沿同一路线驶向同一目的地,甲车先行,一段时间后,乙车开始行驶,甲车到达目的地后,乙车走完了全程的
甲、乙两车都从同一地点沿同一路线驶向同一目的地,甲车先行,一段时间后,乙车开始行驶,甲车到达目的地后,乙车走完了全程的| 4 |
| 9 |
考点:一次函数的应用
专题:
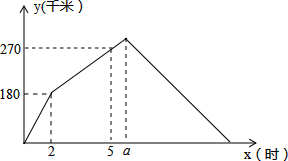
分析:由图象可知①甲先行驶了2小时180千米,则可求得甲车的速度为90千米每小时,②甲车行驶5小时时两车相距270千米,可知在3小时中甲车比乙车多行驶270-180=90千米,故可得每小时甲车比乙车多行驶30千米,即可得到乙车的速度为90-30=60(千米每小时)③甲行驶a小时到达了目的地,则此时乙行驶了(a-2)小时,再利用乙行驶的路程可列关于a的一元一次方程,解出即可.
解答:解:由图象可求得:
甲车的速度为:180÷2=90(千米每小时),
乙车的速度为:90-(270-180)÷(5-2)=60(千米每小时),
由题意可列方程:
×90a=60(a-2),
解得a=6.
故答案为:6.
甲车的速度为:180÷2=90(千米每小时),
乙车的速度为:90-(270-180)÷(5-2)=60(千米每小时),
由题意可列方程:
| 4 |
| 9 |
解得a=6.
故答案为:6.
点评:本题是一道一次函数的综合试题,考查了学生的阅读能力和识图能力的运用,一次函数的图象性质的运用,解答时弄清图象的意义是关键.

练习册系列答案
相关题目
 如图所示,直线AB,CD交于点O,OE平分∠DOB,且∠AOD:∠DOE=3:1,求∠AOC的度数.
如图所示,直线AB,CD交于点O,OE平分∠DOB,且∠AOD:∠DOE=3:1,求∠AOC的度数.
 在平面直角坐标系中放置了一个边长为
在平面直角坐标系中放置了一个边长为 如图,已知∠1=20°,∠2=27°,∠A=52°,则∠BDC的度数是
如图,已知∠1=20°,∠2=27°,∠A=52°,则∠BDC的度数是