题目内容
9.已知如图,在△ABC中,AB=AC,(1)如图(1),若∠α=35°,AD是BC上的高,AD=AE,则∠β=$\frac{35°}{2}$;
(2)如图(2),若∠α=46°,AD是BC上的高,AD=AE,则∠β=23°;
(3)如图(3),D为BC上任意一点.请你思考:在△ABC中,若AB=AC,AD=AE,则∠α和∠β之间有什么关系?如果有,请你写出来,并说明你的理由.
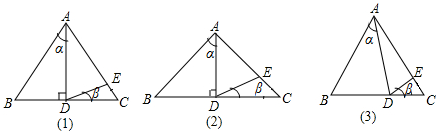
分析 (1)等腰三角形三线合一,所以∠α=35°,又因为AD=AE,所以∠ADE=∠AED=$\frac{145°}{2}$,所以∠β=$\frac{35°}{2}$°;
(2)同理,易证∠ADE=67°,所以∠β=23°;
(3)由于AD=AE,所以∠ADE=∠AED,根据已知,易证∠α+∠B=2∠β+∠C,而∠B=∠C,所以∠α=2∠β.
解答 解解:(1)∵在△ABC中,AB=AC,AD是BC上的高,
∴∠α=∠CAD,
∵∠α=35°,
∴∠α=∠CAD=35°,
∵AD=AE,
∴∠ADE=∠AED=$\frac{145°}{2}$,
∴∠β=90°-$\frac{145°}{2}$=$\frac{35°}{2}$;
故答案为:$\frac{35°}{2}$;
(2)∵在△ABC中,AB=AC,AD是BC上的高,
∴∠α=∠CAD,
∵∠α=46°,
∴∠BAD=∠CAD=46°,
∵AD=AE,
∴∠ADE=∠AED=67°,
∴∠β=23°;
故答案为:23°;
(3)∵AD=AE,
∴∠ADE=∠AED,
∴∠α+∠B=∠ADC=∠ADE+∠β=∠AED+∠β=(∠β+∠C)+∠β=2∠EDC+∠C
又∵AB=AC,
∴∠B=∠C,
∴∠α=2∠β.
点评 本题考查了等腰三角形三线合一的性质,等边对等角的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记性质是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.已知关于x的方程$\frac{m-1}{x-1}=\frac{x}{x-1}$=0的解为非负数,则m的取值范围是( )
| A. | m≥1 | B. | m≥1且m≠2 | C. | m≤1且m≠2 | D. | m≤1 |
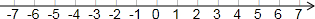 在数轴上表示下列各数并按从小到大的顺序用“<”把这些数连接起来.
在数轴上表示下列各数并按从小到大的顺序用“<”把这些数连接起来.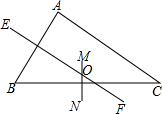 如图,△ABC中,EF是AB的垂直平分线,MN是BC的垂直平分线,EF与MN相交于点O.求证:点O必在AC的垂直平分线上.
如图,△ABC中,EF是AB的垂直平分线,MN是BC的垂直平分线,EF与MN相交于点O.求证:点O必在AC的垂直平分线上.