题目内容
8.小颖在学习“两点之间线段最短”查阅资料时发现:△ABC内总存在一点P与三个顶点的连线的夹角相等,此时该点到三个顶点的距离之和最小.【特例】如图1,点P为等边△ABC的中心,将△ACP绕点A逆时针旋转60°得到△ADE,从而有DE=PC,连接PD得到PD=PA,同时∠APB+∠APD=120°+60°=180°,∠ADP+∠ADE=180°,即B、P、D、E四点共线,故PA+PB+PC=PD+PB+DE=BE.在△ABC中,另取一点P′,易知点P′与三个顶点连线的夹角不相等,可证明B、P′、D′、E四点不共线,所以P′A+P′B+P′C>PA+PB+PC,即点P到三个顶点距离之和最小.

【探究】(1)如图2,P为△ABC内一点,∠APB=∠BPC=120°,证明PA+PB+PC的值最小;
【拓展】(2)如图3,△ABC中,AC=6,BC=8,∠ACB=30°,且点P为△ABC内一点,求点P到三个顶点的距离之和的最小值.
分析 (1)将△ACP绕点A逆时针旋转60°得到△ADE,可得PC=DE,再证△APD为等边三角形得PA=PD、∠APD=∠ADP=60°,由∠APB=∠BPC=120°知B、P、D、E四点共线,根据两点间线段最短即可得答案;
(2)分别以AB、BC为边在△ABC外作等边三角形,连接CD、AE交于点P,先证△ABE≌△DBC可得CD=AE、∠BAE=∠BDC,继而知∠APO=∠OBD=60°,在DO上截取DQ=AP,再证△ABP≌△DBQ可得BP=BQ、∠PBA=∠QBD,从而可证△PBQ为等边三角形,得PB=PQ,由PA+PB+PC=DQ+PQ+PC=CD=AE,Rt△ACE中根据勾股定理即可得AE的长,从而可得答案.
解答 解:(1)如图1,将△ACP绕点A逆时针旋转60°得到△ADE,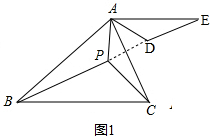
∴∠PAD=60°,△PAC≌△DAE,
∴PA=DA、PC=DE、∠APC=∠ADE=120°,
∴△APD为等边三角形,
∴PA=PD,∠APD=∠ADP=60°,
∴∠APB+∠APD=120°+60°=180°,∠ADP+∠ADE=180°,即B、P、D、E四点共线,
∴PA+PB+PC=PD+PB+DE=BE.
∴PA+PB+PC的值最小.
(2)方法一:如图2,分别以AB、BC为边在△ABC外作等边三角形,连接CD、AE交于点P,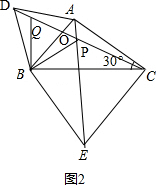
∴AB=DB、BE=BC=8、∠ABD=∠EBC=60°,
∴∠ABE=∠DBC,
在△ABE和△DBC中,
∵$\left\{\begin{array}{l}{AB=DB}\\{∠ABE=∠DBC}\\{BE=BC}\end{array}\right.$,
∴△ABE≌△DBC(SAS),
∴CD=AE、∠BAE=∠BDC,
又∵∠AOP=∠BOD,
∴∠APO=∠OBD=60°,
在DO上截取DQ=AP,连接BQ,
在△ABP和△DBQ中,
∵$\left\{\begin{array}{l}{AB=DB}\\{∠BAP=∠BDQ}\\{AP=DQ}\end{array}\right.$,
∴△ABP≌△DBQ(SAS),
∴BP=BQ,∠PBA=∠QBD,
又∵∠QBD+∠QBA=60°,
∴∠PBA+∠QBA=60°,即∠PBQ=60°,
∴△PBQ为等边三角形,
∴PB=PQ,
则PA+PB+PC=DQ+PQ+PC=CD=AE,
在Rt△ACE中,∵AC=6、CE=8,
∴AE=CD=10,
故点P到三个顶点的距离之和的最小值为10.
方法二:如图3,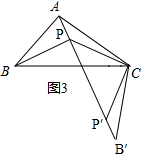
由(2)知,当∠APB=∠APC=∠BPC=120°时,AP+BP+PC的值最小,
把△CPB绕点C逆时针旋转60°得△CP′B′,
由(2)知A、P、P′、B′共线,且AP+BP+PC=AB′,∠PCB=∠P′CB,
∴∠PCB+∠PCA=∠P′CB+∠PCA=30°,
∴∠ACB′=90°,
∴AB′=$\sqrt{A{C}^{2}+B′{C}^{2}}$=$\sqrt{A{C}^{2}+B{C}^{2}}$=10
点评 本题主要考查旋转变换的性质、全等三角形的判定与性质、等边三角形的判定与性质等知识点,将待求线段的和通过旋转变换及全等三角形的性质转化为同一直线上的线段来求是解题的关键.

 如图,在正方形ABCD中,AB=2$\sqrt{2}$,连接AC,以点C为圆心、AC长为半径画弧,点E在BC的延长线上,则阴影部分的面积为( )
如图,在正方形ABCD中,AB=2$\sqrt{2}$,连接AC,以点C为圆心、AC长为半径画弧,点E在BC的延长线上,则阴影部分的面积为( )| A. | 6π-4 | B. | 8π-8 | C. | 10π-4 | D. | 12π-8 |
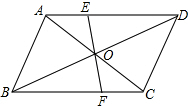 如图,已知平行四边形ABCD的两条对角线相交于点O,过点O的直线与AD,BC分别相交于E,F,则下列结论不正确的是( )
如图,已知平行四边形ABCD的两条对角线相交于点O,过点O的直线与AD,BC分别相交于E,F,则下列结论不正确的是( )| A. | OE=OF | B. | △DOE≌△BOF | C. | S△ABC=S△BCD | D. | EF=AC |
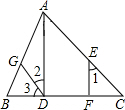 如图,已知AD⊥BC,EF⊥BC,∠3=∠C,求证:∠1=∠2.
如图,已知AD⊥BC,EF⊥BC,∠3=∠C,求证:∠1=∠2. 将如图所示的牌面数字分别是1,2,3,4的四张扑克牌背面朝上,洗匀后放在桌面上.
将如图所示的牌面数字分别是1,2,3,4的四张扑克牌背面朝上,洗匀后放在桌面上.