Question

17．如图1，在等腰Rt△ABC中，∠ACB=90°，AC=BC；在等腰Rt△DCE中，∠DCE=90°，CD=CE；点D、E分别在边BC、AC上，连接AD、BE，点N是线段BE的中点，连接CN与AD交于点G．
（1）若CN=6.5，CE=5，求BD的值；
（2）把等腰Rt△DCE绕点C转至如图2位置，点N是线段BE的中点，延长NC交AD于点H，求证：CN⊥AD．
（3）把等腰Rt△DCE绕点C转至如图3位置，点N是线段BE的中点，请问（2）中的结论还成立吗？若成立，请给出证明，若不成立，请说明理由．

Answer 1

分析 （1）根据直角三角形的性质得到BE=2CN=13，根据勾股定理得到BC=$\sqrt{B{E}^{2}-C{E}^{2}}$=5，即可得到结论；
（2）如图2，延长CN到F使FN=CN，连接BF，通过证明△CEN≌△BNF，得到CE=BF，∠F=∠ECN，推出∠CBF=∠DCA，证得△ACD≌△BCF，根据全等三角形的性质得到∠DAC=∠BCF，等量代换即可得到结论．
（3）结论不变．证明方法类似．

解答 （1）解：如图1中，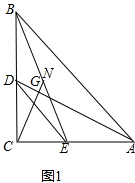

∵∠ACB=90°，点N是线段BE的中点，
∴BE=2CN=13，
∵CE=5，
∴BC=$\sqrt{B{E}^{2}-C{E}^{2}}$=$\sqrt{1{3}^{2}-{5}^{2}}$=12，
∵CD=CE=5，
∴BD=BC-CD=12-5=7；
（2）如图2中，延长CN到F使FN=CN，连接BF，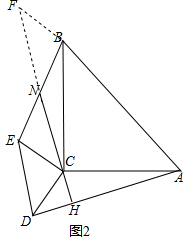

在△CEN与△BFN中，
$\left\{\begin{array}{l}{CN=FN}\\{∠CNE=∠BNF}\\{EN=BN}\end{array}\right.$，
∴△CEN≌△BNF，
∴CE=BF，∠F=∠ECN
∵∠CBF=180°-∠F-∠BCF，∠DCA=360°-∠DCE-∠ACB-∠BCE=180°-∠ECF-∠BCF，
∴∠CBF=∠DCA，
∵CE=CD，
∴BF=CD，
在△ACD与△BCF中，
$\left\{\begin{array}{l}{CD=BF}\\{∠ACD=∠FBC}\\{AC=BC}\end{array}\right.$，
∴△ACD≌△BCF，
∴∠DAC=∠BCF，
∵∠BCF+∠ACH=90°，
∴∠CAH+∠ACH=90°，
∴∠AHC=90°，
∴CN⊥AD．

（3）结论仍然成立．如图3中，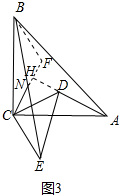

证明：延长CN到F使FN=CN，连接BF，延长AD交CF于H．
在△CEN与△BFN中，
$\left\{\begin{array}{l}{CN=FN}\\{∠CNE=∠BNF}\\{EN=BN}\end{array}\right.$，
∴△CEN≌△BNF，
∴CE=BF，∠F=∠ECN
∵∠CBF=180°-∠F-∠BCF=180°-∠FCE-∠BCF=180°-∠BCE=90°-∠ACE，∠DCA=90°-∠ACE，
∴∠CBF=∠DCA，
∵CE=CD，
∴BF=CD，
在△ACD与△BCF中，
$\left\{\begin{array}{l}{CD=BF}\\{∠ACD=∠FBC}\\{AC=BC}\end{array}\right.$，
∴△ACD≌△BCF，
∴∠DAC=∠BCF，
∵∠BCF+∠ACH=90°，
∴∠CAH+∠ACH=90°，
∴∠AHC=90°，
∴CN⊥AD．

点评 本题考查了全等三角形的判定与性质，等腰直角三角形的性质，三角形的面积公式，正确的作出辅助线是解题的关键，属于中考压轴题．