Question

16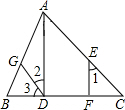．如图，已知AD⊥BC，EF⊥BC，∠3=∠C，求证：∠1=∠2．

Answer 1

分析 根据垂直的定义得到∠ADF=∠EFC=90°，再根据同位角相等，两直线平行得到AD∥EF，利用直线平行的性质有∠2=∠DAC；由∠3=∠C，根据同位角相等，两直线平行得到DG∥AC，再利用直线平行的性质得∠1=∠DAC，最后利用等量代换即可得到结论．

解答 证明：∵AD⊥BC，EF⊥BC，
∴∠ADF=∠EFC=90°，
∴AD∥EF，
∴∠2=∠DAC，
又∵∠3=∠C，
∴DG∥AC，
∴∠1=∠DAC，
∴∠1=∠2．

点评 本题考查了直线平行的判定与性质：同位角相等，两直线平行；两直线平行，内错角相等．