题目内容
17.通过计算比较下列各组数中两个数的大小,在横线上填写“>”“=”或“<”①12<21;②23<32;③34>43;④45>54; ⑤56>65
(2)根据第(1)小题结果经过归纳,可以猜想出nn+1和(n+1)n的大小关系当n=1或2时,nn+1<(n+1)n;当n>2的整数时,nn+1>(n+1)n?
(3)根据上面的归纳猜想得到的一般结论,判断两个数的大小关系:19971998与19981997.
分析 (1)根据乘方的意义求出每个式子的结果,再比较即可.
(2)根据(1)的结果即可得出结论.
(3)根据(2)中结论比较即可.
解答 解:(1)①12<21,
故答案为:<.
②23<32,
故答案为:<.
③34>43,
故答案为:>.
④45>54,
故答案为:>.
⑤56>65,
故答案为:>;
(2)由(1)可知,当n=1或2时,nn+1<(n+1)n;当n>2的整数时,nn+1>(n+1)n.
故答案为:当n=1或2时,nn+1<(n+1)n;当n>2的整数时,nn+1>(n+1)n;
(3)∵n=1997>2,
∴19971998>19981997.
点评 本题考查了有理数的乘方和有理数的大小比较的应用,关键是能得出规律.

练习册系列答案
相关题目
7.若一个一元二次方程的两根为$\sqrt{2}$+1,$\sqrt{2}$-1,则这个方程是( )
| A. | x2+2$\sqrt{2}$x+1=0 | B. | x2-2$\sqrt{2}$x-1=0 | C. | x2-2$\sqrt{2}$x+1=0 | D. | x2+2$\sqrt{2}$x-1=0 |
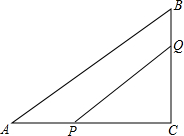 如图,△ABC中,∠C=90°,AB=10cm,AC=8cm,点P从A点出发向点C以2cm/s的速度移动,点Q从B点出发向点C以1cm/s的速度移动,当其中一点首先到达终点时运动停止,若P、Q分别同时从A,B出发,几秒后四边形APQB是△ABC面积的$\frac{2}{3}$?
如图,△ABC中,∠C=90°,AB=10cm,AC=8cm,点P从A点出发向点C以2cm/s的速度移动,点Q从B点出发向点C以1cm/s的速度移动,当其中一点首先到达终点时运动停止,若P、Q分别同时从A,B出发,几秒后四边形APQB是△ABC面积的$\frac{2}{3}$? 在数轴上表示下列各数,并用“<”号连接.(数轴上表示与“<”号连接均写原数)
在数轴上表示下列各数,并用“<”号连接.(数轴上表示与“<”号连接均写原数)