题目内容
1.若整数n使得$\frac{{n}^{2}}{n-2}$也是整数,则满足条件的n有6个.分析 将原式化为n+2+$\frac{4}{n-2}$,由题意可知:$\frac{4}{n-2}$为整数即可.
解答 解:原式=$\frac{{n}^{2}-4+4}{n-2}$=$\frac{{n}^{2}-4}{n-2}+\frac{4}{n-2}$=n+2+$\frac{4}{n+2}$
当$\frac{4}{n-2}$是整数即可满足题意,
故n-2=±1,±2,±4,
n=-2,0,1,3,4,6
故答案为:6
点评 本题考查分式的值,涉及因式分解,一元一次方程的解法,整数的条件.

练习册系列答案
相关题目
13.一个角的两边与另一个角的两边互相垂直,且这两个角之差为40°,那么这两个角分别为( )
| A. | 70°和110° | B. | 80°和120° | C. | 40°和140° | D. | 100°和140° |
10.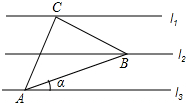 如图,已知l1∥l2∥l3,相邻两条平行直线间的距离相等,若等腰△ABC的三个顶点分别在这三条平行直线上,若∠ACB=90°,则sinα的值是( )
如图,已知l1∥l2∥l3,相邻两条平行直线间的距离相等,若等腰△ABC的三个顶点分别在这三条平行直线上,若∠ACB=90°,则sinα的值是( )
 如图,已知l1∥l2∥l3,相邻两条平行直线间的距离相等,若等腰△ABC的三个顶点分别在这三条平行直线上,若∠ACB=90°,则sinα的值是( )
如图,已知l1∥l2∥l3,相邻两条平行直线间的距离相等,若等腰△ABC的三个顶点分别在这三条平行直线上,若∠ACB=90°,则sinα的值是( )| A. | $\frac{1}{3}$ | B. | $\frac{6}{17}$ | C. | $\frac{{\sqrt{5}}}{5}$ | D. | $\frac{{\sqrt{10}}}{10}$ |
 如图,已知:?ABCD的对角线AC、BD相交于点O,S△BOD=4cm2,求?ABCD的面积.
如图,已知:?ABCD的对角线AC、BD相交于点O,S△BOD=4cm2,求?ABCD的面积. 如图,三个全等的小矩形沿“横-竖-横”排列在一个大的边长分别为23.45、12.34的矩形中,则图中一个小矩形的周长等于23.86.
如图,三个全等的小矩形沿“横-竖-横”排列在一个大的边长分别为23.45、12.34的矩形中,则图中一个小矩形的周长等于23.86.