题目内容
2.先化简,再求值:$\frac{x+3}{{x}^{2}-2x}$÷($\frac{x+8}{{x}^{2}-4x+4}$-$\frac{1}{2-x}$),其中x2-4=0.分析 先根据分式混合运算的法则把原式进行化简,再求出x的值代入进行计算即可.
解答 解:原式=$\frac{x+3}{x(x-2)}$÷($\frac{x+8}{(x-2)^{2}}$+$\frac{1}{x-2}$)
=$\frac{x+3}{x(x-2)}$÷$\frac{x+8+x-2}{{(x-2)}^{2}}$
=$\frac{x+3}{x(x-2)}$÷$\frac{2(x+3)}{{(x-2)}^{2}}$
=$\frac{x+3}{x(x-2)}$•$\frac{(x-2)^{2}}{2(x+3)}$
=$\frac{x-2}{2x}$,
∵x2-4=0,
∴x1=2(舍去),x2=-2,
∴当x=-2时,原式=$\frac{-2-2}{-4}$=1.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
12.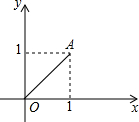 如图,点A的坐标是(1,1),如果将线段OA绕点O按逆时针方向旋转135°,那么点A旋转后的对应点的坐标是( )
如图,点A的坐标是(1,1),如果将线段OA绕点O按逆时针方向旋转135°,那么点A旋转后的对应点的坐标是( )
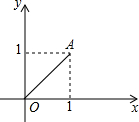 如图,点A的坐标是(1,1),如果将线段OA绕点O按逆时针方向旋转135°,那么点A旋转后的对应点的坐标是( )
如图,点A的坐标是(1,1),如果将线段OA绕点O按逆时针方向旋转135°,那么点A旋转后的对应点的坐标是( )| A. | (-$\sqrt{2}$,0) | B. | (0,-$\sqrt{2}$) | C. | (0,-1) | D. | (-1,0) |
 如图,△ABC中,点D,E,F分别是BC,AD,CE的中点,S△ABC=12,则S△DEF=1.5.
如图,△ABC中,点D,E,F分别是BC,AD,CE的中点,S△ABC=12,则S△DEF=1.5. 将直角三角尺的顶点靠在直尺上,且斜边与这根直尺平行,那么在形成的这个图中(如图),与∠α互余的角共有2个.
将直角三角尺的顶点靠在直尺上,且斜边与这根直尺平行,那么在形成的这个图中(如图),与∠α互余的角共有2个. 如图,如果AB∥CD,则角α、β、γ之间的关系为∠α+∠β-∠γ=180°.
如图,如果AB∥CD,则角α、β、γ之间的关系为∠α+∠β-∠γ=180°.