题目内容
17.先化简,再求值:(x2y+$\frac{1}{2}x{y}^{2}$)-3(xy2-2x2y)-(5x2y-2xy2),其中x=-4,y=$\frac{1}{3}$.分析 首先去掉括号,再合并同类项,然后把x=-4,y=$\frac{1}{3}$代入,求出算式的值是多少即可.
解答 解:(x2y+$\frac{1}{2}x{y}^{2}$)-3(xy2-2x2y)-(5x2y-2xy2)
=x2y+$\frac{1}{2}x{y}^{2}$-3xy2+6x2y-5x2y+2xy2
=(x2y+6x2y-5x2y)+($\frac{1}{2}x{y}^{2}$-3xy2+2xy2)
=2x2y-0.5xy2,
当x=-4,y=$\frac{1}{3}$时,
原式=2${×(-4)}^{2}×\frac{1}{3}-0.5×(-4){×(\frac{1}{3})}^{2}$
=10$\frac{2}{3}+\frac{2}{9}$
=$10\frac{8}{9}$.
点评 此题主要考查了整式的化简求值问题,解答此题的关键是注意去括号时符号的变化.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
5.随着经济的发展,节能与环保问题越来越得到重视,据宁波环境保护局披露:2015年宁波市区节能环保支出将达到18957.74万元.18957.74万元用科学记数法应记为( )
| A. | 18957.74×104元 | B. | 1.895774×107元 | C. | 1.895774×108元 | D. | 1.895774×109元 |
12.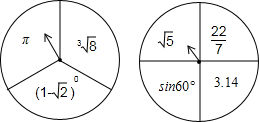 如图所示的两个转盘分别被均匀地分成3个和4个扇形如图所示的两个转盘分别被均匀地分成3个和4个扇形,每个扇形上都标有一个实数.同时自由转动两个转盘,转盘停止后(若指针指在分格线上,则重转),两个指针都落在无理数上的概率是( )
如图所示的两个转盘分别被均匀地分成3个和4个扇形如图所示的两个转盘分别被均匀地分成3个和4个扇形,每个扇形上都标有一个实数.同时自由转动两个转盘,转盘停止后(若指针指在分格线上,则重转),两个指针都落在无理数上的概率是( )
 如图所示的两个转盘分别被均匀地分成3个和4个扇形如图所示的两个转盘分别被均匀地分成3个和4个扇形,每个扇形上都标有一个实数.同时自由转动两个转盘,转盘停止后(若指针指在分格线上,则重转),两个指针都落在无理数上的概率是( )
如图所示的两个转盘分别被均匀地分成3个和4个扇形如图所示的两个转盘分别被均匀地分成3个和4个扇形,每个扇形上都标有一个实数.同时自由转动两个转盘,转盘停止后(若指针指在分格线上,则重转),两个指针都落在无理数上的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{12}$ |
 如图,?ABCD中,∠ABC的平分线分别与AC、AD交于点E、F,且AE:AC=3:8,若AB=3,则DF的长为2.
如图,?ABCD中,∠ABC的平分线分别与AC、AD交于点E、F,且AE:AC=3:8,若AB=3,则DF的长为2.