题目内容
18.解方程x4-6x2+5=0这是一个一元四次方程,通常解法:设x2=y,那么x4=y2,于是原方程可变为y2-6y+5=0,解得:y1=1,y2=5.当y=1时,x2=1,∴x=±1;当y=5时,x2=5,∴x=±$\sqrt{5}$.所以原方程有四个根:x1=1,x2=-1,x3=$\sqrt{5}$,x4=-$\sqrt{5}$.仿照上例对方程x2+$\frac{1}{{x}^{2}}$-3(x+$\frac{1}{x}$)+2=0进行转化,求代数式x+$\frac{1}{x}$的值.分析 先根据完全平方公式变形,设x+$\frac{1}{x}$=y,则方程化为y2-3y=0,求出y即可.
解答 解:x2+$\frac{1}{{x}^{2}}$-3(x+$\frac{1}{x}$)+2=0,
(x+$\frac{1}{x}$)2-2x$•\frac{1}{x}$-3(x+$\frac{1}{x}$)+2=0,
(x+$\frac{1}{x}$)2-3(x+$\frac{1}{x}$)=0,
设x+$\frac{1}{x}$=y,则方程化为:y2-3y=0,
解得:y=3或0,
x+$\frac{1}{x}$=3或0.
点评 本题考查了解一元二次方程的应用,能正确换元是解此题的关键,难度不是很大.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
8.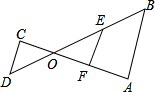 如图,若DC∥FE∥AB,则有( )
如图,若DC∥FE∥AB,则有( )
 如图,若DC∥FE∥AB,则有( )
如图,若DC∥FE∥AB,则有( )| A. | $\frac{OD}{OF}$=$\frac{OC}{OE}$ | B. | $\frac{OF}{OB}$=$\frac{OA}{OC}$ | C. | $\frac{OA}{OC}$=$\frac{OD}{OB}$ | D. | $\frac{CD}{EF}$=$\frac{OD}{OE}$ |
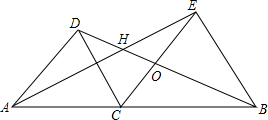 如图,在线段AB的同侧有等边△ACD和等边△CBE,AE、DB交于H.求证:DA2=DH•DB.
如图,在线段AB的同侧有等边△ACD和等边△CBE,AE、DB交于H.求证:DA2=DH•DB.