题目内容
13.如图,在矩形ABCD中,AB:BC=1:2,E是AD上的一点,BE=BC,求∠CED的度数.分析 根据矩形性质得出∠A=∠BCD=90°,AB=CD,AD∥BC,推出BE=2AB,得出∠AEB=30°=∠EBC,求出∠ECB的度数,即可求出答案.
解答 解:∵四边形ABCD是矩形,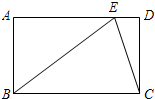
∴∠A=∠BCD=90°,AB=CD,AD∥BC,
∵BE=BC,AB:BC=1:2,
∴BE=2AB,
∴∠AEB=30°,
∵AD∥BC,
∴∠AEB=∠EBC=30°,
∵BE=BC,
∴∠BEC=∠BCE=$\frac{1}{2}$(180°-∠EBC)=75°,
∵∠EDC=90°,
∴∠CED=∠BCE=75°.
点评 本题考查了矩形性质,三角形的内角和定理,平行线性质,等腰三角形的性质,含30度角的直角三角形性质的应用,解此题的关键是求出∠AEB和∠BEC的度数,题目比较好,是一道综合性比较强的题目.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
4.下面的数中,比-2小的数的是( )
| A. | 2 | B. | -1 | C. | 0 | D. | -3 |
1.小雨将平面直角坐标系中的三角形ABC进行平移,得到三角形A′B′C′,已知点A(2,-1)的对应点A′的坐标为(a,-4),点B(5,-2)的对应点B′的坐标为(3,b),则点C(a,b)的对应点C′的坐标为( )
| A. | (3,-4) | B. | (-2,-8) | C. | (0,-5) | D. | 无法确定 |
5.某工程咨询公司技术部门有总工程师1人,工程师1人,技术员7人,见习技术员1人,现需招聘技术员1人,小王前来应征,总经理说:“我们这里的报酬不错,平均工资是每月1900元,你在这里好好干!”小王在公司工作一周后,找到总经理说:“你欺骗了我,我已问过其他技术员,没有一个技术员的工资超过1900元,平均工资怎么可能是每月1900元呢?”总经理说:“平均工资确实是每月1900元.”下表是该部门月工资报表
(1)请你仔细观察表中的数据,讨论该部门员工的月平均工资是多少?总经理是否欺骗了小王?
(2)平均月工资能否客观的反映员工的实际收入?
(3)再仔细观察表中的数据,你认为用什么数据反应一般技术员的实际收入比较合适?
| 员工 | 总工程师 | 工程师 | 技术员A | 技术员B | 技术员C |
| 工资 | 5000 | 4000 | 1800 | 1700 | 1500 |
| 员工 | 技术员D | 技术员E | 技术员F | 技术员G | 见习技术员H |
| 工资 | 1200 | 1200 | 1200 | 1000 | 400 |
(2)平均月工资能否客观的反映员工的实际收入?
(3)再仔细观察表中的数据,你认为用什么数据反应一般技术员的实际收入比较合适?
14.将分式$\frac{x^2}{x+y}$中的x、y的值同时扩大3倍,则分式的值( )
| A. | 扩大3倍 | B. | 缩小到原来的$\frac{1}{3}$ | C. | 保持不变 | D. | 扩大9倍 |
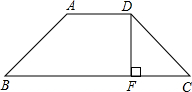 如图,四边形ABCD中,AD∥BC,且AB=CD,DF⊥BC于F,AD=DF=FC=1,将它剪两刀,剪成4块,然后拼成一个正方形,想一想,应该怎样剪?画出图形来说明.
如图,四边形ABCD中,AD∥BC,且AB=CD,DF⊥BC于F,AD=DF=FC=1,将它剪两刀,剪成4块,然后拼成一个正方形,想一想,应该怎样剪?画出图形来说明.