题目内容
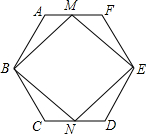 如图,正六边形ABCDEF的半径为4,M、N分别为边AF、CD的中点,则四边形MBNE的面积为
如图,正六边形ABCDEF的半径为4,M、N分别为边AF、CD的中点,则四边形MBNE的面积为考点:正多边形和圆
专题:
分析:如图,作辅助线,首先求出BE、MN的长;证明四边形MBNE为菱形,问题即可解决.
解答: 解:如图,连接OM、ON、OB、OC、OD、OE;
解:如图,连接OM、ON、OB、OC、OD、OE;
∵六边形ABCDEF是正六边形,
∴∠BOC=∠COD=∠DOE=
×360°=60°,
∠BCN=∠EDN,BC=CD=DE;而OB=OC,
∴△OBC为等边三角形,∠BOC+∠COD+∠DOE=180°,
∴BC=OB=4,B、O、E三点共线,BE=2OB=8;
同理可求MN=BE=8;
在△BCN与△EDN中,
,
∴△BCN≌△EDN(SAS),
∴BN=EN;同理可求NE=EM=MB,
∴四边形MBNE是菱形,
∵在△OCD中,ON=2
,
∴MN=4
,
∴S菱形MBNE=
BE•MN=
×8×4
=16
.
 解:如图,连接OM、ON、OB、OC、OD、OE;
解:如图,连接OM、ON、OB、OC、OD、OE;∵六边形ABCDEF是正六边形,
∴∠BOC=∠COD=∠DOE=
| 1 |
| 6 |
∠BCN=∠EDN,BC=CD=DE;而OB=OC,
∴△OBC为等边三角形,∠BOC+∠COD+∠DOE=180°,
∴BC=OB=4,B、O、E三点共线,BE=2OB=8;
同理可求MN=BE=8;
在△BCN与△EDN中,
|
∴△BCN≌△EDN(SAS),
∴BN=EN;同理可求NE=EM=MB,
∴四边形MBNE是菱形,
∵在△OCD中,ON=2
| 3 |
∴MN=4
| 3 |
∴S菱形MBNE=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
点评:该题主要考查了圆内接正多边形的性质及其应用问题;解题的关键是灵活运用有关定理来分析、判断、推理或解答.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
下列实数
,0,π,
,
,
中是无理数的有( )
| 1 |
| 2 |
| 4 |
| 1 |
| 3 |
| 5 |
| A、1个 | B、2个 | C、3个 | D、4个 |
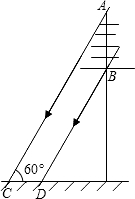 一根电线杆的接线柱部分AB在阳光下的投影CD的长为1.2,太阳光线与地面的夹角∠ACD=60°,则AB的长为( )
一根电线杆的接线柱部分AB在阳光下的投影CD的长为1.2,太阳光线与地面的夹角∠ACD=60°,则AB的长为( )| A、12 | ||||
| B、0.6 | ||||
C、
| ||||
D、
|
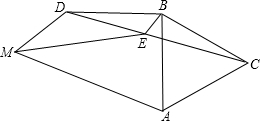 如图,已知AB=BD,∠ABD=90°,△ABC为等边三角形,∠AMD=60°,BE平分∠ABD.
如图,已知AB=BD,∠ABD=90°,△ABC为等边三角形,∠AMD=60°,BE平分∠ABD. 二次函数y=ax2+bx+c(a≠0)的图象如图,下列4个结论中结论正确的有
二次函数y=ax2+bx+c(a≠0)的图象如图,下列4个结论中结论正确的有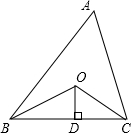 如图所示,已知△ABC的周长是20,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=3,则△ABC的面积是
如图所示,已知△ABC的周长是20,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=3,则△ABC的面积是 如图,在平面直角坐标系中,已知点A(0,1),(-
如图,在平面直角坐标系中,已知点A(0,1),(- 如图,已知
如图,已知