题目内容
边心距为10cm的正方形的外接圆的面积为 ．
考点：正多边形和圆
专题：
分析：如图，作辅助线，根据题意结合图形求出⊙O的半径，即可解决问题．
解答：
解：如图，连接AC、BD；
∵四边形ABCD为正方形，
∴∠BCD=90°，∠BOC=90°；
∴BD为⊙O的直径；
又∵OB=OC，OM⊥BC，
∴BM=CM，而∠BOC=90°，
∴BC=2OM=20；设圆O的半径为λ，
由勾股定理得：λ2+λ2=202，
∴λ2=200，
∴边心距为10cm的正方形的外接圆的面积
=πλ2=200π（cm2）．
解：如图，连接AC、BD；∵四边形ABCD为正方形，
∴∠BCD=90°，∠BOC=90°；
∴BD为⊙O的直径；
又∵OB=OC，OM⊥BC，
∴BM=CM，而∠BOC=90°，
∴BC=2OM=20；设圆O的半径为λ，
由勾股定理得：λ2+λ2=202，
∴λ2=200，
∴边心距为10cm的正方形的外接圆的面积
=πλ2=200π（cm2）．
点评：该题主要考查了正多边形及其外接圆的性质及其应用问题；解题的关键是深刻分析、大胆猜测、合情推理、科学论证．
练习册系列答案
相关题目
数轴上点A，B，C，D对应的有理数都是整数，若点A对应有理数a，
点B对应有理数b，且b-2a=7，则数轴上原点应是（ ）
点B对应有理数b，且b-2a=7，则数轴上原点应是（ ）| A、A点 | B、B点 | C、C点 | D、D点 |
已知：如图，CD⊥AB，EF⊥AB，垂足分别为D、F，CD=EF，AD=BF．求证：∠A=∠B．
如图，在∠AOB的两边OA，OB上分别取OM=ON，OD=OE，DN和EM相交于点C．求证：DN=EM．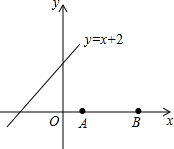
三圣乡一菜地的平面直角坐标系如图，菜地中两个灌溉喷头A（1，0），B（3，0），在菜地边缘有一水渠l：y=x+2，现要在水渠上修一水阀P，并向A，B铺设输水管，若要求P到A，B距离相等，则P的坐标为
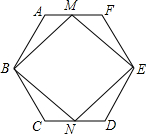如图，正六边形ABCDEF的半径为4，M、N分别为边AF、CD的中点，则四边形MBNE的面积为
如图：在Rt△ABC中，∠ACB=90°，P为AB上一点，Q为BC上一点，且PQ⊥AB，若△BPQ的面积等于四边形APQC的面积的