题目内容
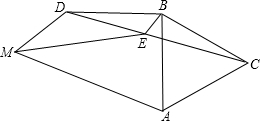 如图,已知AB=BD,∠ABD=90°,△ABC为等边三角形,∠AMD=60°,BE平分∠ABD.
如图,已知AB=BD,∠ABD=90°,△ABC为等边三角形,∠AMD=60°,BE平分∠ABD.(1)求∠BEC的度数;
(2)探究MD+MA与ME的关系.
考点:全等三角形的判定与性质
专题:
分析:(1)易求得∠DBC=150°,BD=BC,即可求得∠BCE度数,再根据BE平分∠ABD可求得∠CBE度数,根据三角形内角和为180°即可解题;
(2)连接AE,延长MA于F使FA=FM,连接EF,易证△BDE≌△BAE,可得AE=DE,∠AEB=∠BED=120°,进而可以求证△EDM≌△EAF,可得ME=MF,∠EMF=∠EFM=30°,即可求得MF和ME大小关系即可解题.
(2)连接AE,延长MA于F使FA=FM,连接EF,易证△BDE≌△BAE,可得AE=DE,∠AEB=∠BED=120°,进而可以求证△EDM≌△EAF,可得ME=MF,∠EMF=∠EFM=30°,即可求得MF和ME大小关系即可解题.
解答:解:

(1)∵AB=BD,△ABC是等边三角形,
∴AD=BD=AC,
∴BD=BC,
∴△BDC是等腰三角形,
∵△ABD是等腰直角三角形,∠ABC=60°,
∴∠BCE=15°,
∵BE平分∠ABD,
∴∠EBC=105°,
∴∠BEC=60°,
(2)连接AE,延长MA于F使FA=FM,连接EF,
∵在△BDE和△BAE中,
,
∴△BDE≌△BAE,(SAS)
∴AE=DE,∠AEB=∠BED=120°,
∴∠AED=120°,
∵∠AED+∠AMD=60°+120°=180°,
∴∠EAM+∠EDM=180°,
∵∠EAM+∠EAF=180°,
∴∠EDM=∠EAF,
∵在△EDM和△EAF中,
,
∴△EDM≌△EAF,(SAS)
∴ME=MF,∠EMF=∠EFM=30°,
∴MD+MA=MF=
ME.

(1)∵AB=BD,△ABC是等边三角形,
∴AD=BD=AC,
∴BD=BC,
∴△BDC是等腰三角形,
∵△ABD是等腰直角三角形,∠ABC=60°,
∴∠BCE=15°,
∵BE平分∠ABD,
∴∠EBC=105°,
∴∠BEC=60°,
(2)连接AE,延长MA于F使FA=FM,连接EF,
∵在△BDE和△BAE中,
|
∴△BDE≌△BAE,(SAS)
∴AE=DE,∠AEB=∠BED=120°,
∴∠AED=120°,
∵∠AED+∠AMD=60°+120°=180°,
∴∠EAM+∠EDM=180°,
∵∠EAM+∠EAF=180°,
∴∠EDM=∠EAF,
∵在△EDM和△EAF中,
|
∴△EDM≌△EAF,(SAS)
∴ME=MF,∠EMF=∠EFM=30°,
∴MD+MA=MF=
| 3 |
点评:本题考查了全等三角形的判定,考查了全等三角形对应边、对应角相等的性质,本题中求证△BDE≌△BAE和△EDM≌△EAF是解题的关键.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
若规定a△b=a÷b×
,则(-90)△
的结果为( )
| -1 |
| b |
| 1 |
| 30 |
| A、81000 | B、-81000 |
| C、90 | D、-90 |
下列等式成立的是( )
| A、|a|+|-a|=0 |
| B、-a-a=0 |
| C、|-a|-|a|=0 |
| D、-a-|a|=0 |
 已知:如图,CD⊥AB,EF⊥AB,垂足分别为D、F,CD=EF,AD=BF.求证:∠A=∠B.
已知:如图,CD⊥AB,EF⊥AB,垂足分别为D、F,CD=EF,AD=BF.求证:∠A=∠B. 如图,在∠AOB的两边OA,OB上分别取OM=ON,OD=OE,DN和EM相交于点C.求证:DN=EM.
如图,在∠AOB的两边OA,OB上分别取OM=ON,OD=OE,DN和EM相交于点C.求证:DN=EM.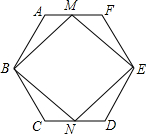 如图,正六边形ABCDEF的半径为4,M、N分别为边AF、CD的中点,则四边形MBNE的面积为
如图,正六边形ABCDEF的半径为4,M、N分别为边AF、CD的中点,则四边形MBNE的面积为 在△ABC中,∠BAC=90°,AD⊥BC于D,E为AC的中点,DE交BA的延长线于F,求证:AB:AC=BF:DF.
在△ABC中,∠BAC=90°,AD⊥BC于D,E为AC的中点,DE交BA的延长线于F,求证:AB:AC=BF:DF.