题目内容
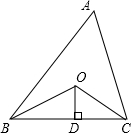 如图所示,已知△ABC的周长是20,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=3,则△ABC的面积是
如图所示,已知△ABC的周长是20,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=3,则△ABC的面积是考点:角平分线的性质
专题:
分析:根据角平分线上的点到角的两边的距离相等可得点O到AB、AC、BC的距离都相等,从而可得到△ABC的面积等于周长的一半乘以OD,然后列式进行计算即可求解.
解答: 解:如图,连接OA,
解:如图,连接OA,
∵OB、OC分别平分∠ABC和∠ACB,
∴点O到AB、AC、BC的距离都相等,
∵△ABC的周长是20,OD⊥BC于D,且OD=3,
∴S△ABC=
×20×3=30.
故答案为:30.
 解:如图,连接OA,
解:如图,连接OA,∵OB、OC分别平分∠ABC和∠ACB,
∴点O到AB、AC、BC的距离都相等,
∵△ABC的周长是20,OD⊥BC于D,且OD=3,
∴S△ABC=
| 1 |
| 2 |
故答案为:30.
点评:本题考查的是角平分线的性质,熟知角平分线上的点到角的两边的距离相等的性质及判断出三角形的面积与周长的关系是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列等式成立的是( )
| A、|a|+|-a|=0 |
| B、-a-a=0 |
| C、|-a|-|a|=0 |
| D、-a-|a|=0 |
下列说法:①有一个角为50°的两个等腰三角形相似;②有一个角为100°的两个等腰三角形相似;③有一个锐角相等的两个直角三角形相似;④两个等边三角形相似.其中正确的有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
 如图,数轴上A、B上两点分别对应有理数a、b,则下列结论正确的是( )
如图,数轴上A、B上两点分别对应有理数a、b,则下列结论正确的是( )| A、a+b>0 |
| B、ab>0 |
| C、-b>a |
| D、|a|>|b| |
 如图,在∠AOB的两边OA,OB上分别取OM=ON,OD=OE,DN和EM相交于点C.求证:DN=EM.
如图,在∠AOB的两边OA,OB上分别取OM=ON,OD=OE,DN和EM相交于点C.求证:DN=EM.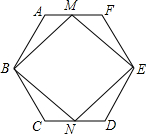 如图,正六边形ABCDEF的半径为4,M、N分别为边AF、CD的中点,则四边形MBNE的面积为
如图,正六边形ABCDEF的半径为4,M、N分别为边AF、CD的中点,则四边形MBNE的面积为
 在△ABC中,∠BAC=90°,AD⊥BC于D,E为AC的中点,DE交BA的延长线于F,求证:AB:AC=BF:DF.
在△ABC中,∠BAC=90°,AD⊥BC于D,E为AC的中点,DE交BA的延长线于F,求证:AB:AC=BF:DF.