题目内容
4.观察下列各数:-$\frac{1}{2}$,$\frac{2}{3}$,-$\frac{3}{4}$,$\frac{4}{5}$,-$\frac{5}{6}$,…,根据它们的排列规律写出第2017个数为-$\frac{2017}{2018}$.分析 分子是从1开始连续的自然数,分母比分子多1,奇数位置为负,偶数位置为正,由此得出第n个数为(-1)n$\frac{n}{n+1}$,进一步代入求得答案即可.
解答 解:∵第n个数为(-1)n$\frac{n}{n+1}$,
∴第2017个数为-$\frac{2017}{2018}$.
故答案为:-$\frac{2017}{2018}$.
点评 此题考查数字的变化规律,发现数字之间的联系,找出数字之间的运算规律,利用规律解决问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.根据国家发改委实施“阶梯电价”的有关文件要求,某市结合地方实际,决定从2016年4月1日起对居民生活用电试行“阶梯电价”收费,具体收费标准见表:
2016年5月份,该市居民甲用电100度,交电费80元;居民乙用电200度,交电费170元.
(1)表中,a=0.8,b=1;
(2)试行“阶梯电价”收费以后,该市一户居民2016年8月份平均电价每度为0.9元,求该用户8月用电多少度?
| 一户居民一个月用电量的范围 | 电费价格(单位:元/度) |
| 不超过150度 | a |
| 超过150度的部分 | b |
(1)表中,a=0.8,b=1;
(2)试行“阶梯电价”收费以后,该市一户居民2016年8月份平均电价每度为0.9元,求该用户8月用电多少度?
13. 学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,碟子的个数与碟子的高度的关系如下表:
学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,碟子的个数与碟子的高度的关系如下表:
(1)当桌子上放有x个碟子时,碟子的高度是1.8x+1.2;(用含x的式子表示)
(2)分别从三个方向看桌子上摆放的四摞碟子的形状如上图所示,厨房师傅想把它们整齐地叠成一摞,求叠成一摞后碟子的高度.
 学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,碟子的个数与碟子的高度的关系如下表:
学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,碟子的个数与碟子的高度的关系如下表:| 碟子的个数 | 碟子的高度 (单位:cm) |
| 1 | 3 |
| 2 | 3+1.8 |
| 3 | 3+3.6 |
| 4 | 3+5.4 |
| … | … |
(2)分别从三个方向看桌子上摆放的四摞碟子的形状如上图所示,厨房师傅想把它们整齐地叠成一摞,求叠成一摞后碟子的高度.
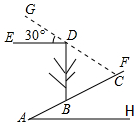 如图,斜坡AF的坡度为5:12,斜坡AF上一棵与水平面垂直的大树BD在阳光照射下,在斜坡上的影长BC=6.5米,此时光线与水平线恰好成30°角,求大树BD的高.(结果精确的0.1米,参考数据$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图,斜坡AF的坡度为5:12,斜坡AF上一棵与水平面垂直的大树BD在阳光照射下,在斜坡上的影长BC=6.5米,此时光线与水平线恰好成30°角,求大树BD的高.(结果精确的0.1米,参考数据$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732) 如图,点A、B都在数轴上,且AB=6
如图,点A、B都在数轴上,且AB=6 如图,已知△ABE≌△ACD,且∠B=∠C,则下列结论:
如图,已知△ABE≌△ACD,且∠B=∠C,则下列结论: