题目内容
19.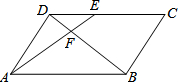 如图,在平行四边形ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,S△DEF:S△ABF=4:25,则S△ADF:S四边形BCEF为( )
如图,在平行四边形ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,S△DEF:S△ABF=4:25,则S△ADF:S四边形BCEF为( )| A. | 10:31 | B. | 10:21 | C. | 4:25 | D. | 4:21 |
分析 先证明△DEF∽△BAF,得出$\frac{DE}{AB}$=$\frac{EF}{AF}$=$\frac{2}{5}$,得出$\frac{{S}_{△DEF}}{{S}_{△ADF}}$=$\frac{EF}{AF}$=$\frac{2}{5}$=$\frac{4}{10}$,再得出$\frac{{S}_{△ADF}}{{S}_{△ABD}}$=$\frac{10}{35}$,即可得出结果.
解答 解:∵四边形ABCD是平行四边形,
∴AB=DC,DC∥AB,S△BCD=S△ABD,
∴△DEF∽△BAF,
∴$\frac{{S}_{△DEF}}{{S}_{△BAF}}$=$(\frac{DE}{AB})^{2}$=$\frac{4}{25}$,
∴$\frac{DE}{AB}$=$\frac{EF}{AF}$=$\frac{2}{5}$,
∴$\frac{{S}_{△DEF}}{{S}_{△ADF}}$=$\frac{EF}{AF}$=$\frac{2}{5}$=$\frac{4}{10}$,
∴$\frac{{S}_{△ADF}}{{S}_{△ABD}}$=$\frac{10}{10+25}$=$\frac{10}{35}$,
∴$\frac{{S}_{△ADF}}{{S}_{四边形BCEF}}$=$\frac{10}{35-4}$=$\frac{10}{31}$;
故选:A.
点评 本题考查了平行四边形的性质、相似三角形的判定与性质以及面积的计算方法;熟练掌握平行四边形的性质,证明三角形相似是解决问题的关键.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
7.把一张矩形的ABCD白纸,AB=3,BC=3$\sqrt{3}$,按图(一)沿AE折叠,使B落在AD边上的,再沿MN折使点A落在C处,则折痕MN长为( )
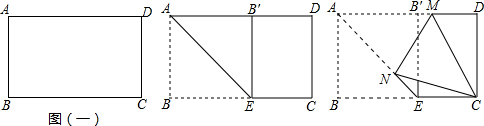

| A. | 6-2$\sqrt{3}$ | B. | 3$\sqrt{2}$-6 | C. | 6$\sqrt{3}$-6 | D. | $\sqrt{3}$+$\sqrt{2}$ |
8.下列轴对称图形中,对称轴条数是四条的图形是( )
| A. |  | B. |  | C. |  | D. |  |
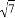 -1,那么m的取值范围是( ).
-1,那么m的取值范围是( ). 的解为正数,则m的取值范围是__.
的解为正数,则m的取值范围是__. 如图,在6×6的正方形网格中,△ABC的顶点在格点上,请仅用无刻度的直尺分别在图①、图②中画出△ABC的AB边上的高.
如图,在6×6的正方形网格中,△ABC的顶点在格点上,请仅用无刻度的直尺分别在图①、图②中画出△ABC的AB边上的高. 如图中所示是一圆锥形的零件经过轴的剖面,它的腰长等于圆锥的母线长,底边长等于圆锥底面的直径,按图中表明的尺寸求这个零件的母线长为36.
如图中所示是一圆锥形的零件经过轴的剖面,它的腰长等于圆锥的母线长,底边长等于圆锥底面的直径,按图中表明的尺寸求这个零件的母线长为36.