题目内容
16.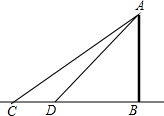 如图所示,对岸有一铁塔AB,在C处测得塔顶A的仰角为30°,向塔前进16米到达D,在D处测得A的仰角为40°,求铁塔AB的高.(结果保留整数)
如图所示,对岸有一铁塔AB,在C处测得塔顶A的仰角为30°,向塔前进16米到达D,在D处测得A的仰角为40°,求铁塔AB的高.(结果保留整数)
分析 首先根据题意分析图形;本题涉及到两个直角三角形,设AB=x(米),再利用CD=BC-BD=16的关系,进而可解即可求出答案.
解答 解:在Rt△ABD中,
∵∠ADB=40°,
∴BD=$\frac{AB}{tan40°}$=$\frac{AB}{0.84}$,
在Rt△ABC中,
∵∠ACB=30°,
∴BC=$\sqrt{3}$AB.
设AB=x(米),
∵CD=16,
∴BC=$\frac{x}{0.84}$+16.
∴$\frac{x}{0.84}$+16=$\sqrt{3}$x
∴x≈9,
即铁塔AB的高为9米.
点评 本题考查俯角、仰角的定义,要求学生能借助俯角、仰角构造直角三角形并结合图形利用三角函数解直角三角形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.若m>n,t为任意实数,则下列各不等式中,恒成立的是( )
| A. | mt2>nt2 | B. | mt2≥nt2 | C. | mt>nt | D. | mt<nt |
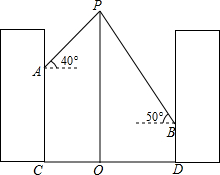 如图,某学校的两栋教学楼正中间有一个旗杆OP,旗杆底端O与两楼底部C、D在同一直线上,且OC=OD=10米,小明在图中左侧搂上点C的正上方A处测得旗杆顶端P的仰角为40°,小刚在图中右侧楼上点D的正上方B处测得旗杆顶端P的仰角为50°,侧得AC=8米,试求旗秆OP的长度和BD的长(参考数据:tan40°≈0.84,tan50°≈1.19,结果精确到0.1米)
如图,某学校的两栋教学楼正中间有一个旗杆OP,旗杆底端O与两楼底部C、D在同一直线上,且OC=OD=10米,小明在图中左侧搂上点C的正上方A处测得旗杆顶端P的仰角为40°,小刚在图中右侧楼上点D的正上方B处测得旗杆顶端P的仰角为50°,侧得AC=8米,试求旗秆OP的长度和BD的长(参考数据:tan40°≈0.84,tan50°≈1.19,结果精确到0.1米)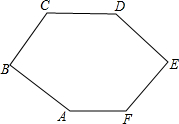 如图,CD∥AF,∠CDE=∠BAF,AB⊥BC,∠C=128°,∠E=80°,求∠F的度数.
如图,CD∥AF,∠CDE=∠BAF,AB⊥BC,∠C=128°,∠E=80°,求∠F的度数.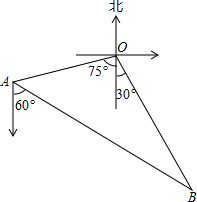 如图,编号为2307和2308的两艘海监船同时从港口O出发外出某岛海域巡航,2307海监船沿南偏西75°方向以每小时15$\sqrt{2}$海里的速度航行,2308海监船沿南偏东30°方向以每小时15海里的速度航行,航行1小时后,2307海监船在A处收到消息,2308海监船附近发现疑似敌舰,于是2307海监船迅速改变航向和速度,以匀速沿南偏东60°方向追赶2308海监船,正好在B处追上,2307海监船追赶2308海监船的速度为多少海里/时?
如图,编号为2307和2308的两艘海监船同时从港口O出发外出某岛海域巡航,2307海监船沿南偏西75°方向以每小时15$\sqrt{2}$海里的速度航行,2308海监船沿南偏东30°方向以每小时15海里的速度航行,航行1小时后,2307海监船在A处收到消息,2308海监船附近发现疑似敌舰,于是2307海监船迅速改变航向和速度,以匀速沿南偏东60°方向追赶2308海监船,正好在B处追上,2307海监船追赶2308海监船的速度为多少海里/时?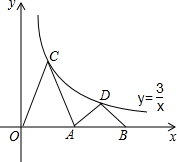 如图,点C、D在双曲线y=$\frac{3}{x}$(x>0)上,点A、B在x轴上,且OA=AB,CO=CA,DA=DB,则S△OCA+S△ADB=4.
如图,点C、D在双曲线y=$\frac{3}{x}$(x>0)上,点A、B在x轴上,且OA=AB,CO=CA,DA=DB,则S△OCA+S△ADB=4.