Question

20．如图，正方形ABCD中，E为BD上一点，F为BC上一点，EF=EC．
（1）求证：AF=$\sqrt{2}$EF；
（2）求证：AB+BF=$\sqrt{2}$BE．

Answer 1

分析 （1）如图连接AE．由△BEA≌△BEC，推出AE=EC=EF，∠BAE=∠BCE，由EF=EC，推出∠EFC=∠ECF，由∠BFE+∠EFC=180°，推出∠BAE+∠BFE=180°，推出∠ABC+∠AEF=360°-（∠BAE+∠BFE）=180°，由∠ABC=90°，推出∠AEF=90°，推出△AEF是等腰直角三角形，即可解决问题．
（2）延长BC到M，使得CM=BF，由△EFB≌△ECM，推出EB=EM，∠EBF=∠M=45°，推出△EBM是等腰直角三角形，推出BM=$\sqrt{2}$BE，由BF=CM，推出BC=FM=AB，推出AB+BF=FM+BF=BM=$\sqrt{2}$BE．

解答 证明：（1）如图连接AE．
∵四边形ABCD是正方形，
∴∠ABC=90°，∠ABD=∠CBD=45°，AB=CB，
在△BEA和△BEC中，
$\left\{\begin{array}{l}{BE=BE}\\{∠EBA=∠EBC}\\{BC=BA}\end{array}\right.$，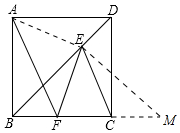
∴△BEA≌△BEC，
∴AE=EC=EF，∠BAE=∠BCE，
∵EF=EC，
∴∠EFC=∠ECF，
∵∠BFE+∠EFC=180°，
∴∠BAE+∠BFE=180°，
∴∠ABC+∠AEF=360°-（∠BAE+∠BFE）=180°，
∵∠ABC=90°，
∴∠AEF=90°，
∴△AEF是等腰直角三角形，
∴AF=$\sqrt{2}$AE．

（2）延长BC到M，使得CM=BF，
∵∠EFC=∠ECF，
∴∠EFB=∠ECM，
在△EFB和△ECM中，
$\left\{\begin{array}{l}{EF=EC}\\{∠EFB=∠ECM}\\{BF=CM}\end{array}\right.$，
∴△EFB≌△ECM，
∴EB=EM，∠EBF=∠M=45°，
∴△EBM是等腰直角三角形，
∴BM=$\sqrt{2}$BE，
∵BF=CM，
∴BC=FM=AB，
∴AB+BF=FM+BF=BM=$\sqrt{2}$BE，

点评 本题考查正方形的性质、全等三角形的判定和性质、等腰三角形的判定和性质、等腰直角三角形的性质和判定等知识，解题的关键是学会添加辅助线，构造全等三角形解决问题，属于中考常考题型．