题目内容
15.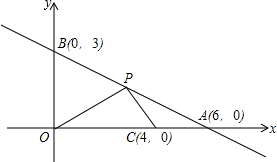 如图,直线AB与x轴、y轴分别交于点A(6,0)、B(0,3),P是线段AB上的一个动点(点P与A、B不重合),点C的坐标为(4,0).
如图,直线AB与x轴、y轴分别交于点A(6,0)、B(0,3),P是线段AB上的一个动点(点P与A、B不重合),点C的坐标为(4,0).(1)求直线AB所对应的函数关系式.
(2)设动点P的坐标为(m,n),△PAC的面积为S.
①当PC=PO时,求点P的坐标.
②写出S与m的函数关系式及自变量m的取值范围,并求出使S△PAC=S△PBO时点P的坐标.
分析 (1)利用待定系数法即可求得一次函数的解析式;
(2)①当PC=PO时,点P在CO的垂直平分线上,则P的横坐标即可求得,代入直线解析式求得纵坐标;
②根据三角形的面积公式即可用m表示出S△PAC和S△PBO,即可列方程求得m的值,进而求得P的坐标.
解答 解:(1)设直线AB所对应的函数关系式为y=kx+b(k≠0),
∴$\left\{\begin{array}{l}{b=3}\\{6k+b=0}\end{array}\right.$解得$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=3}\end{array}\right.$,
∴直线AB所对应的函数关系式为y=-$\frac{1}{2}$x+3;
(2)①∵PC=PO,
∴点P在CO的垂直平分线上,
又∵点C的坐标为(4,0),
∴点P的横坐标m=2,
∵点P在直线y=-$\frac{1}{2}$x+3上,
∴n=2,
∴点P的坐标为(2,2);
②∵P(m,n)在y=-$\frac{1}{2}$x+3上,则-$\frac{1}{2}$m+3=n,
∴S=$\frac{1}{2}$OC•n=$\frac{1}{2}$×4×(-$\frac{1}{2}$m+3),
即S=-$\frac{1}{2}$m+3(0<m<6).
S△PBO=$\frac{1}{2}$OB•m=$\frac{1}{2}$×3m,
又∵S△PAC=S△PBO,
∴-$\frac{1}{2}$m+3=$\frac{1}{2}$×3m,
解得:m=$\frac{3}{2}$.
∴点P的坐标为($\frac{3}{2}$,$\frac{9}{4}$).
点评 本题考查了待定系数法求函数的解析式,以及三角形的面积公式,用m表示出S△PAC和S△PBO是关键.

 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案| A. | y=2x-1 | B. | y=$\frac{3}{x}$ | C. | y=2x | D. | y=$\frac{2}{x}$ |
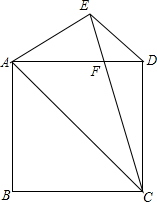 如图,正方形ABCD中,过D作DE∥AC,∠ACE=30°,CE交AD于点F,求证:AC=EC.
如图,正方形ABCD中,过D作DE∥AC,∠ACE=30°,CE交AD于点F,求证:AC=EC. 拱桥截面是一条抛物线,如图所示,现测得水面宽AB=16m,拱顶O到水面的距离为8m,在图中的直角坐标系内,拱桥所在抛物线的解析式是y=-$\frac{1}{8}$x2.
拱桥截面是一条抛物线,如图所示,现测得水面宽AB=16m,拱顶O到水面的距离为8m,在图中的直角坐标系内,拱桥所在抛物线的解析式是y=-$\frac{1}{8}$x2.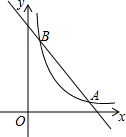 如图,一次函数y=kx+b(k≠0)与反比例函数y=$\frac{4}{x}$(x>0)的图象交于A(m,1)B(1,n)两点
如图,一次函数y=kx+b(k≠0)与反比例函数y=$\frac{4}{x}$(x>0)的图象交于A(m,1)B(1,n)两点