题目内容
7.(1)计算:|-5|+(π-3.1)0-($\frac{1}{2}$)-1+$\sqrt{4}$(2)先化简,$\frac{2}{{a}^{2}-4}$•($\frac{{a}^{2}+4}{4a}$-1)÷($\frac{1}{2}$-$\frac{1}{a}$),请你为a的值选择一个喜欢的数字,并求值.
(3)解方程:$\frac{x}{x+2}$-$\frac{x+2}{x-2}$=$\frac{8}{{x}^{2}-4}$.
分析 (1)根据实数的运算顺序,从左向右依次计算,求出算式|-5|+(π-3.1)0-($\frac{1}{2}$)-1+$\sqrt{4}$的值是多少即可.
(2)首先计算小括号里面的,然后从左向右依次计算,将算式$\frac{2}{{a}^{2}-4}$•($\frac{{a}^{2}+4}{4a}$-1)÷($\frac{1}{2}$-$\frac{1}{a}$)化简,然后把喜欢的数字a=1代入化简后的算式,求出算式的值是多少即可.
(3)通过观察,可得最简公分母是x2-4,方程两边同时乘以最简公分母,即可把分式方程化为整式方程,然后根据整式方程的求解方法,求出方程$\frac{x}{x+2}$-$\frac{x+2}{x-2}$=$\frac{8}{{x}^{2}-4}$的解即可,注意验根.
解答 解:(1)|-5|+(π-3.1)0-($\frac{1}{2}$)-1+$\sqrt{4}$
=5+1-2+2
=6
(2)$\frac{2}{{a}^{2}-4}$•($\frac{{a}^{2}+4}{4a}$-1)÷($\frac{1}{2}$-$\frac{1}{a}$)
=$\frac{2}{{a}^{2}-4}$•$\frac{{(a-2)}^{2}}{4a}$÷$\frac{a-2}{2a}$
=$\frac{a-2}{2a(a+2)}$÷$\frac{a-2}{2a}$
=$\frac{1}{a+2}$
我喜欢的数字是1,
当a=1时,
原式=$\frac{1}{1+2}=\frac{1}{3}$.
(3)去分母,可得
x(x-2)-(x+2)2=8,
整理,可得
x+2=0,
解得x=-2,
∵当x=-2时,
x+2=-2+2=0,不符合题意,
∴x=-2不是方程的解,
∴方程$\frac{x}{x+2}$-$\frac{x+2}{x-2}$=$\frac{8}{{x}^{2}-4}$无解.
点评 (1)此题主要考查了分式的化简求值问题,注意化简时不能跨度太大,而缺少必要的步骤.
(2)此题还考查了实数的运算,要熟练掌握,解答此题的关键是要明确:在进行实数运算时,和有理数运算一样,要从高级到低级,即先算乘方、开方,再算乘除,最后算加减,有括号的要先算括号里面的,同级运算要按照从左到有的顺序进行.另外,有理数的运算律在实数范围内仍然适用.
(3)此题还考查了负整数指数幂的运算,要熟练掌握,解答此题的关键是要明确:①a-p=$\frac{1}{{a}^{p}}$(a≠0,p为正整数);②计算负整数指数幂时,一定要根据负整数指数幂的意义计算;③当底数是分数时,只要把分子、分母颠倒,负指数就可变为正指数.
(4)此题还考查了零指数幂的运算,要熟练掌握,解答此题的关键是要明确:①a0=1(a≠0);②00≠1.
(5)此题还考查了解分式方程问题,要熟练掌握,解答此题的关键是要明确解分式方程的步骤:①去分母;②求出整式方程的解;③检验;④得出结论.

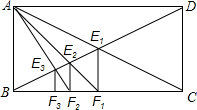 如图,矩形ABCD中,BC=1,连接AC与BD交于点E1,过E1作E1F1⊥BC于F1,连接AF1交BD于E2,过E2作E2F2⊥BC于F2,连接AF2交BD于E3,过E3作E3F3⊥BC于F3,…,以此类推,则BFn(其中n为正整数)的长为( )
如图,矩形ABCD中,BC=1,连接AC与BD交于点E1,过E1作E1F1⊥BC于F1,连接AF1交BD于E2,过E2作E2F2⊥BC于F2,连接AF2交BD于E3,过E3作E3F3⊥BC于F3,…,以此类推,则BFn(其中n为正整数)的长为( )| A. | $\frac{n}{n+1}$ | B. | $\frac{1}{n+1}$ | C. | $\frac{n+1}{n+2}$ | D. | $\frac{n+1}{n+3}$ |
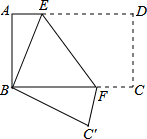 如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,若AB=1,BC=2,则△ABE和△BC′F的周长之和为( )
如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,若AB=1,BC=2,则△ABE和△BC′F的周长之和为( )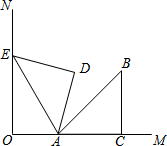 如图,ON⊥OM,等腰直角三角形ACB中,∠ACB=90°,边AC在OM上,将△ACB绕点A逆时针旋转75°,使得点B的对应点E恰好落在ON上,则$\frac{OA}{EA}$=$\frac{1}{2}$.
如图,ON⊥OM,等腰直角三角形ACB中,∠ACB=90°,边AC在OM上,将△ACB绕点A逆时针旋转75°,使得点B的对应点E恰好落在ON上,则$\frac{OA}{EA}$=$\frac{1}{2}$.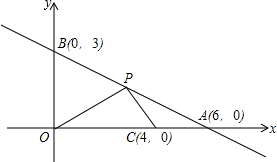 如图,直线AB与x轴、y轴分别交于点A(6,0)、B(0,3),P是线段AB上的一个动点(点P与A、B不重合),点C的坐标为(4,0).
如图,直线AB与x轴、y轴分别交于点A(6,0)、B(0,3),P是线段AB上的一个动点(点P与A、B不重合),点C的坐标为(4,0).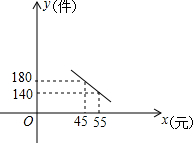 大学生王强积极响应“自主创业”的好种,准备投资销售一种进价为每件4元的小家电,通过试营销发现,当销售单价在40元至60元之间(含40元和60元)时,每月的销售量y(件)与销售单价x(元)之间的关系可近似地看作一次函数,其图象如图所示.
大学生王强积极响应“自主创业”的好种,准备投资销售一种进价为每件4元的小家电,通过试营销发现,当销售单价在40元至60元之间(含40元和60元)时,每月的销售量y(件)与销售单价x(元)之间的关系可近似地看作一次函数,其图象如图所示.