题目内容
3.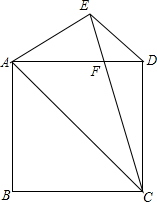 如图,正方形ABCD中,过D作DE∥AC,∠ACE=30°,CE交AD于点F,求证:AC=EC.
如图,正方形ABCD中,过D作DE∥AC,∠ACE=30°,CE交AD于点F,求证:AC=EC.
分析 作EG⊥AC于G,DH⊥AC于H,证明四边形DEGH是平行四边形,得出EG=DH,由含30°角的直角三角形的性质得出EG=$\frac{1}{2}$EC,由正方形的性质得出△ADC是等腰直角三角形,证出DH=$\frac{1}{2}$AC,即可得出结论.
解答 证明:作EG⊥AC于G,DH⊥AC于H,如图所示: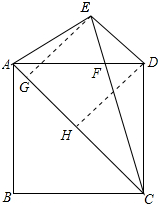 则EG∥DH,
则EG∥DH,
∵DE∥AC,
∴四边形DEGH是平行四边形,
∴EG=DH,
∵∠ACE=30°,
∴EG=$\frac{1}{2}$EC,
∵四边形ABCD是正方形,
∴AD=CD,∠ADC=90°,
即△ADC是等腰直角三角形,
∴AH=CH,
∴DH=$\frac{1}{2}$AC,
∴AC=EC.
点评 本题考查了正方形的性质、平行四边形的判定与性质、等腰直角三角形的性质、含30°角的直角三角形的性质;熟练掌握正方形的性质,并能进行推理论证是解决问题的关键.

练习册系列答案
相关题目
14.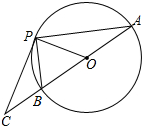 如图,AB为⊙O的直径,直线PC与⊙O相切于点P,交AB的延长线于C,∠PBC=120°,则∠PCB=( )
如图,AB为⊙O的直径,直线PC与⊙O相切于点P,交AB的延长线于C,∠PBC=120°,则∠PCB=( )
 如图,AB为⊙O的直径,直线PC与⊙O相切于点P,交AB的延长线于C,∠PBC=120°,则∠PCB=( )
如图,AB为⊙O的直径,直线PC与⊙O相切于点P,交AB的延长线于C,∠PBC=120°,则∠PCB=( )| A. | 15° | B. | 30° | C. | 45° | D. | 60° |
8.根据世界贸易组织(WTO)秘书处初步统计数据,2013年中国货物进出口总额为4160000000000美元,超过美国成为世界第一货物贸易大国.将这个数据用科学记数法可以记为( )美元.
| A. | 4.16×1012 | B. | 4.16×1013 | C. | 0.416×1012 | D. | 416×1010 |
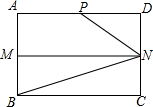 如图,在矩形ABCD中,AB=4,AD=6,M,N分别是AB,CD的中点,P是AD上的点,且∠PNB=3∠CBN.
如图,在矩形ABCD中,AB=4,AD=6,M,N分别是AB,CD的中点,P是AD上的点,且∠PNB=3∠CBN. 如图:在△ABC中,点D,E在BC上,且AD=AE,BD=CE,∠ADE=∠AED,求证:AB=AC.
如图:在△ABC中,点D,E在BC上,且AD=AE,BD=CE,∠ADE=∠AED,求证:AB=AC.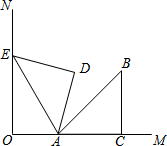 如图,ON⊥OM,等腰直角三角形ACB中,∠ACB=90°,边AC在OM上,将△ACB绕点A逆时针旋转75°,使得点B的对应点E恰好落在ON上,则$\frac{OA}{EA}$=$\frac{1}{2}$.
如图,ON⊥OM,等腰直角三角形ACB中,∠ACB=90°,边AC在OM上,将△ACB绕点A逆时针旋转75°,使得点B的对应点E恰好落在ON上,则$\frac{OA}{EA}$=$\frac{1}{2}$.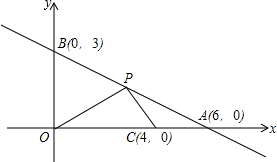 如图,直线AB与x轴、y轴分别交于点A(6,0)、B(0,3),P是线段AB上的一个动点(点P与A、B不重合),点C的坐标为(4,0).
如图,直线AB与x轴、y轴分别交于点A(6,0)、B(0,3),P是线段AB上的一个动点(点P与A、B不重合),点C的坐标为(4,0).