Question

13．如图，5个同样大小的正方形拼成一个长方形，求∠ABC+∠ADC+∠ACB的度数．

Answer 1

分析 利用勾股定理分别计算出△ACD和△ADB的各个边长，根据有三边比值相等的两三角形相似可判定△ACD和△ADB相定理即可求出似，再根据相似三角形的性质：对应角相等和三角形外角和定理即可求出∠ABC+∠ADC+∠ACB的度数．

解答 解：设每个小正方形的边长为1，
由勾股定理得：AC=$\sqrt{2}$，AD=$\sqrt{5}$，AB=$\sqrt{10}$，
又∵DC=1，BD=5，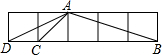
∴$\frac{AD}{BD}$=$\frac{\sqrt{5}}{5}$，$\frac{AC}{AB}=\frac{\sqrt{2}}{\sqrt{10}}=\frac{\sqrt{5}}{5}$，$\frac{CD}{AD}$=$\frac{1}{\sqrt{5}}$=$\frac{\sqrt{5}}{5}$，
∴$\frac{AD}{BD}$=$\frac{AC}{AB}=\frac{CD}{AD}$，
∴△ADC∽△BDA，
∴∠DAC=∠ABD，
∵∠ACB=45°，
∴∠ACB=∠DAC+∠ADB=45°，
∴∠ABC+∠ADC+∠ACB=90°．

点评 本题考查了相似三角形的判定和相似三角形的性质以及勾股定理的运用和三角形的外角和不相邻的两内角之间的关系．