题目内容
20.当已知A(-2,y1),B(-1,y2),C(-5,y3)在抛物线y=-$\frac{1}{2}$x2-3x-π上,则y1,y2,y3之间的大小关系是( )| A. | y1<y2<y3 | B. | y2<y1<y3 | C. | y2=y3<y1 | D. | y3<y2<y1 |
分析 先求出二次函数y=-$\frac{1}{2}$x2-3x-π的图象的对称轴,然后判断出A(-2,y1),B(-1,y2),C(-5,y3)在抛物线上的位置,再求解.
解答 解:∵二次函数y=-$\frac{1}{2}$x2-3x-π中a=-$\frac{1}{2}$<0,
∴抛物线开口向下,对称轴为x=-$\frac{b}{2a}$=-3,
∵A(-2,y1),B(-1,y2)中横坐标均大于-3,
∴它们在对称轴的右侧y2<y1,C(-5,y3)中横坐标小于-3,
∵它在对称轴的左侧,它关于x=-3的对称点为-1,
∵a<0时,抛物线开口向下,在对称轴的右侧y随x的增大而减小,
∴y3=y2<y1,
故选C.
点评 本题考查了二次函数图象上点的坐标特征,解题的关键是找到二次函数的对称轴;掌握二次函数y=ax2+bx+c(a≠0)的图象性质.

练习册系列答案
相关题目
8.“直角都相等”与“相等的角是直角”是( )
| A. | 互为逆命题 | B. | 互逆定理 | C. | 公理 | D. | 假命题 |
 (1)已知一个多边形的内角和是外角和的两倍,求它的边数.
(1)已知一个多边形的内角和是外角和的两倍,求它的边数. 如图,在四边形ABCD中,连接AC,恰有∠ACD=∠ADC,点F在AB上,连接DF,交AC于点G,在DG上取一点E,连接AE,使得△AED≌△ABC,若∠CAD=90°,∠BCA=20°.
如图,在四边形ABCD中,连接AC,恰有∠ACD=∠ADC,点F在AB上,连接DF,交AC于点G,在DG上取一点E,连接AE,使得△AED≌△ABC,若∠CAD=90°,∠BCA=20°.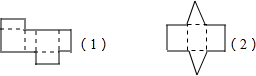 下面是两种立体图形的展开图.请分别写出这两个立体图形的名称:
下面是两种立体图形的展开图.请分别写出这两个立体图形的名称: