题目内容
6.观察下列一组数:$\frac{1}{4},\frac{1}{3},\frac{3}{8},\frac{2}{5},…$,它们是按一定的规律排列的,那么这一组数的第100个数是$\frac{50}{101}$.分析 根据已知数据得出分母是从4开始的连续奇数,分子是从1开始的连续自然数,进而得出答案即可.
解答 解:∵$\frac{1}{4},\frac{1}{3},\frac{3}{8},\frac{2}{5},…$,即$\frac{1}{4}$,$\frac{2}{6}$,$\frac{3}{8}$,$\frac{4}{10}$,
∴这一组数的第100个数是$\frac{100}{4+2×100-2}$=$\frac{100}{202}$=$\frac{50}{101}$.
故答案为:$\frac{50}{101}$.
点评 此题主要考查了数字变化规律,根据已知得出分子与分母的变化是解题关键.

练习册系列答案
相关题目
14.下列条件不能用来判定四边形ABCD是平行四边形的是( )
| A. | ∠A:∠B:∠C:∠D=1:4:1:4 | B. | AB∥CD,AD=BC | ||
| C. | AB=CD,AD=BC | D. | AB∥CD,AD∥CB |
1.已知点A的坐标是(a,b),若a+b<0,ab>0,则它在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
11.下列基本图形是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
18.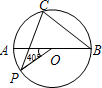 如图所示,AB为⊙O的直径,P点为其半圆上一点,∠POA=40°,C为另一半圆上任意一点(不含A、B),则∠PCB的度数为( )
如图所示,AB为⊙O的直径,P点为其半圆上一点,∠POA=40°,C为另一半圆上任意一点(不含A、B),则∠PCB的度数为( )
 如图所示,AB为⊙O的直径,P点为其半圆上一点,∠POA=40°,C为另一半圆上任意一点(不含A、B),则∠PCB的度数为( )
如图所示,AB为⊙O的直径,P点为其半圆上一点,∠POA=40°,C为另一半圆上任意一点(不含A、B),则∠PCB的度数为( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |