题目内容
如果直线y=-2x平行移动后,与双曲线y=-
恰交于点(m,3),那么平移后得到的直线是函数 的图象.
| 3 |
| x |
考点:反比例函数与一次函数的交点问题,一次函数图象与几何变换
专题:计算题
分析:由于两函数均过(m,3),将(m,3)代入y=-
得到m的值,将求得的(m,3)代入y=-2x+b,求出b的值,从而得到函数的解析式.
| 3 |
| x |
解答:解:将(m,3)代入y=-
得,3=-
,m=-1,
设函数解析式为y=-2x+b,
将(-1,3)代入y=-2x+b得,3=2+b,b=1,
则函数解析式为y=-2x+1.
故答案为y=-2x+1.
| 3 |
| x |
| 3 |
| m |
设函数解析式为y=-2x+b,
将(-1,3)代入y=-2x+b得,3=2+b,b=1,
则函数解析式为y=-2x+1.
故答案为y=-2x+1.
点评:本题考查了反比例函数与一次函数的交点问题及一次函数的平移变换,要知道,平行的两个一次函数的比例系数k相同.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
甲、乙、丙、丁四名运动员参加4×100米接力赛,如果甲必须安排在第二棒,那么,这四名运动员在比赛中的接棒顺序有( )
| A、4种可能 | B、5种可能 |
| C、6种可能 | D、8种可能 |
对关于x的方程ax2+bx+c=0(a≠0).下列结论中:
①方程的解为x=
;②若a+c=0,方程ax2+bx+c=0有两个不等的实数根;
③若方程ax2+bx+c=0有两个不等的实数根,则方程x2+bx+ac=0也一定有两个不等的实数根;④若二次三项式ax2+bx+c是完全平方式,则方程ax2+bx+c=0必有两相等实根;其中正确的结论是( )
①方程的解为x=
-b±
| ||
| 2a |
③若方程ax2+bx+c=0有两个不等的实数根,则方程x2+bx+ac=0也一定有两个不等的实数根;④若二次三项式ax2+bx+c是完全平方式,则方程ax2+bx+c=0必有两相等实根;其中正确的结论是( )
| A、①③④ | B、①②④ |
| C、②③④ | D、①②③ |
若a、b、c为实数,且
=
=
=k,则下列四个点中,不可能在正比例函数y=kx的图象上的点是( )
| c |
| a+b |
| b |
| a+c |
| a |
| b+c |
| A、(-5,5) |
| B、(3,3) |
| C、(-4,-2) |
| D、(0,0) |
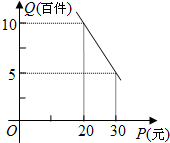 单价P(元)的关系如图所示;维持企业的正常运转每月需最低生活费外的各种开支2000元.
单价P(元)的关系如图所示;维持企业的正常运转每月需最低生活费外的各种开支2000元.