题目内容
我们将能完全覆盖三角形的最小圆称为该三角形的最小覆盖圆,求:能覆盖住边长为
,
,4的三角形的最小圆的半径.
| 13 |
| 13 |
考点:三角形的外接圆与外心
专题:
分析:根据等腰三角形的三边长可知,此等腰三角形是锐角三角形,因此能盖住三角形的最小圆应该是三角形的外接圆;可过等腰三角形的顶角顶点作圆的直径,通过勾股定理和相交弦定理求出此圆的外接圆半径.
解答: 解:如图;△ABC中,AB=AC=
解:如图;△ABC中,AB=AC=
,BC=4;
由于△ABC是锐角三角形,因此能覆盖此三角形的最小圆应该是△ABC的外接圆⊙O;
过A作⊙O的直径AE,交BC于D;
在Rt△ABD中,AB=
,BD=2,
由勾股定理得:AD=3;
由相交弦定理知:BD2=AD•DE,即DE=BD2÷AD=
;
故⊙O的半径最小为:
(AD+DE)=
×(3+
)=
.
 解:如图;△ABC中,AB=AC=
解:如图;△ABC中,AB=AC=| 13 |
由于△ABC是锐角三角形,因此能覆盖此三角形的最小圆应该是△ABC的外接圆⊙O;
过A作⊙O的直径AE,交BC于D;
在Rt△ABD中,AB=
| 13 |
由勾股定理得:AD=3;
由相交弦定理知:BD2=AD•DE,即DE=BD2÷AD=
| 4 |
| 3 |
故⊙O的半径最小为:
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| 3 |
| 13 |
| 6 |
点评:此题考查了等腰三角形的性质、勾股定理、垂径定理、相交弦定理等知识的综合应用,首先判断出△ABC的形状是解题的关键.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
下列说法中正确的是( )
| A、正数加负数,和为0 |
| B、两个数的和为负数,则这两个数一定是负数 |
| C、两个有理数相加,等于它们的绝对值相加 |
| D、两个正数相加和为正,两个负数相加和为负 |
 如图,AB、CD交于E,且AC=BD,∠A+∠B=180°,求证:CE=DE.
如图,AB、CD交于E,且AC=BD,∠A+∠B=180°,求证:CE=DE.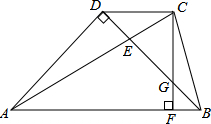 如图,梯形ABCD中,CD∥AB,△ABD为等腰直角三角形,AC=AB,AC与BD相交于E点,CF⊥AB于点F,交BD于G点,下列结论:(1)BE=BC;(2)BC=
如图,梯形ABCD中,CD∥AB,△ABD为等腰直角三角形,AC=AB,AC与BD相交于E点,CF⊥AB于点F,交BD于G点,下列结论:(1)BE=BC;(2)BC=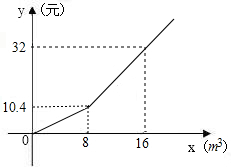 为了节约用水,某城市制定了两种如图用水标准,设某户每月用水量为xm3,应缴水费为y元,请你根据图象回答下列问题:
为了节约用水,某城市制定了两种如图用水标准,设某户每月用水量为xm3,应缴水费为y元,请你根据图象回答下列问题: