题目内容
如图所示,①中多边形(边数为12)是由正三角形“扩展”而来的,②中多边形是由正方形“扩展”而来的,…,依此类推,由正n边形“扩展”而来的多边形的边数记为an(n≥3).则a7的值是 ,当
+
+
+…+
的结果是
时,n的值是 .

| 1 |
| a3 |
| 1 |
| a4 |
| 1 |
| a5 |
| 1 |
| an |
| 97 |
| 300 |

考点:规律型:图形的变化类
专题:
分析:结合图形观察数字,发现:a3=12=3×4,a4=20=4×5,a5=5×6=30,…进一步得到an=n(n+1);在计算的时候,根据
+
+…+
=
-
+
-
+…+
-
…进行简便计算得出关于n的方程求解即可.
| 1 |
| 3×4 |
| 1 |
| 4×5 |
| 1 |
| n(n+1) |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| n |
| 1 |
| n+1 |
解答:解:由图可知a3=12=3×4,a4=20=4×5,a5=5×6=30,…an=n(n+1),
则a7的值是7×8=56;
+
+
+…+
=
+
+…+
=
-
+
-
+…+
-
=
=
解得n=99.
故答案为:56,99.
则a7的值是7×8=56;
| 1 |
| a3 |
| 1 |
| a4 |
| 1 |
| a5 |
| 1 |
| an |
| 97 |
| 300 |
| 1 |
| 3×4 |
| 1 |
| 4×5 |
| 1 |
| n(n+1) |
=
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| n |
| 1 |
| n+1 |
=
| n-2 |
| 3(n+1) |
| 97 |
| 300 |
解得n=99.
故答案为:56,99.
点评:此题考查了图形的变化规律,注意从特殊推广到一般,找出规律,利用规律解决问题.

练习册系列答案
相关题目
已知水星的半径约为24 400 000m,该数据用科学记数法表示为( )
| A、0.244×108m |
| B、2.44×106m |
| C、2.44×107m |
| D、24.4×106m |
抛物线y=x2-mx-m2+1的图象过原点,则m为( )
| A、0 | B、1 | C、-1 | D、±1 |
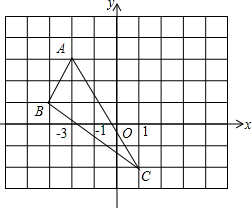 如图,△ABC的三个顶点的坐标分别是A(-2,3),B(-3,1),C(1,-2).
如图,△ABC的三个顶点的坐标分别是A(-2,3),B(-3,1),C(1,-2).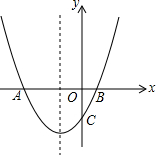 如图,抛物线y=
如图,抛物线y=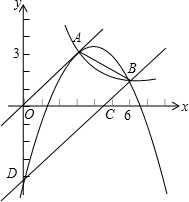 如图,已知正比例函数和反比例函数的图象都经过点A(3,3).
如图,已知正比例函数和反比例函数的图象都经过点A(3,3).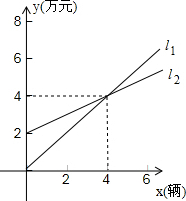 如图,l1反映了神州装载机厂一天的销售收入与销售量之间的函数关系,l
如图,l1反映了神州装载机厂一天的销售收入与销售量之间的函数关系,l