题目内容
16.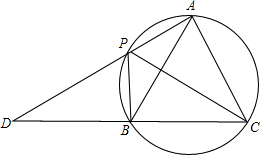 如图,A,P,B,C是圆上的四个点,∠APC=∠CPB=60°,AP,CB的延长线相交于点D.
如图,A,P,B,C是圆上的四个点,∠APC=∠CPB=60°,AP,CB的延长线相交于点D.(1)求证:△ABC是等边三角形;
(2)若∠PAC=90°,AB=2$\sqrt{3}$,求PD的长.
分析 (1)由圆周角定理可知∠ABC=∠BAC=60°,从而可证得△ABC是等边三角形;
(2)由△ABC是等边三角形可得出“AC=BC=AB=2$\sqrt{3}$,∠ACB=60°”,在直角三角形PAC和DAC通过特殊角的正、余切值即可求出线段AP、AD的长度,二者作差即可得出结论.
解答 (1)证明:∵∠ABC=∠APC,∠BAC=∠BPC,∠APC=∠CPB=60°,
∴∠ABC=∠BAC=60°,
∴△ABC是等边三角形.
(2)解:∵△ABC是等边三角形,AB=2$\sqrt{3}$,
∴AC=BC=AB=2$\sqrt{3}$,∠ACB=60°.
在Rt△PAC中,∠PAC=90°,∠APC=60°,AC=2$\sqrt{3}$,
∴AP=$\frac{AC}{tan60°}$=2.
在Rt△DAC中,∠DAC=90°,AC=2$\sqrt{3}$,∠ACD=60°,
∴AD=AC•tan∠ACD=6.
∴PD=AD-AP=6-2=4.
点评 本题考查了圆周角定理、等边三角形的判定及性质以及特殊角的三角函数值,解题的关键是:(1)找出三角形内两角都为60°;(2)通过解直角三角形求出线段AD和AP得长度.本题属于基础题,难度不大,解决该题型题目时,通过解直角三角形找出各边长度,再根据边与边之间的关系求出结论即可.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
1.下列计算结果正确的是( )
| A. | 6x6÷2x3=3x2 | B. | x2+x3=x5 | C. | (-3x2y)2=-9x4y2 | D. | x•x2=x3 |
5.若t为实数,关于x的方程x2-4x+t-2=0的两个非负实数根为a、b,则代数式(a2-1)(b2-1)的最小值是( )
| A. | -15 | B. | -16 | C. | 15 | D. | 16 |
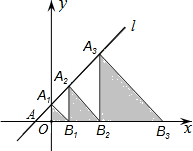 如图,在平面直角坐标系中,直线l:y=x+2交x轴于点A,交y轴于点A1,点A2,A3,…在直线l上,点B1,B2,B3,…在x轴的正半轴上,若△A1OB1,△A2B1B2,△A3B2B3,…,依次均为等腰直角三角形,直角顶点都在x轴上,则第n个等腰直角三角形AnBn-1Bn顶点Bn的横坐标为2n+1-2.
如图,在平面直角坐标系中,直线l:y=x+2交x轴于点A,交y轴于点A1,点A2,A3,…在直线l上,点B1,B2,B3,…在x轴的正半轴上,若△A1OB1,△A2B1B2,△A3B2B3,…,依次均为等腰直角三角形,直角顶点都在x轴上,则第n个等腰直角三角形AnBn-1Bn顶点Bn的横坐标为2n+1-2. 如图,已知∠CAB=∠DBA,∠CBD=∠DAC.
如图,已知∠CAB=∠DBA,∠CBD=∠DAC.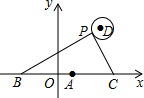 如图,在平面直角坐标系中,已知点A(1,0),B(1-a,0),C(1+a,0)(a>0),点P在以D(4,4)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则a的最大值是6.
如图,在平面直角坐标系中,已知点A(1,0),B(1-a,0),C(1+a,0)(a>0),点P在以D(4,4)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则a的最大值是6. 在平面直角坐标系中,△ABC三个顶点坐标为A(-$\sqrt{3}$,0)、B($\sqrt{3}$,0)、C(0,3).
在平面直角坐标系中,△ABC三个顶点坐标为A(-$\sqrt{3}$,0)、B($\sqrt{3}$,0)、C(0,3).