题目内容
5.若t为实数,关于x的方程x2-4x+t-2=0的两个非负实数根为a、b,则代数式(a2-1)(b2-1)的最小值是( )| A. | -15 | B. | -16 | C. | 15 | D. | 16 |
分析 a,b是关于x的一元二次方程x2-4x+t-2=0的两个非负实根,根据根与系数的关系,化简(a2-1)(b2-1)即可求解.
解答 解:∵a,b是关于x的一元二次方程x2-4x+t-2=0的两个非负实根,
∴可得a+b=4,ab=t-2≥0,△=16-4(t-2)≥0.
解$\left\{\begin{array}{l}{t-2≥0}\\{16-4(t-2)≥0}\end{array}\right.$得:2≤t≤6
(a2-1)(b2-1)=(ab)2-(a2+b2)+1=(ab)2-(a+b)2+2ab+1,
∴(a2-1)(b2-1),
=(t-2)2-16+2(t-2)+1,
=(t-1)2-16,
∵2≤t≤6,
∴当t=2时,(t-1)2取最小值,最小值为1,
∴代数式(a2-1)(b2-1)的最小值是1-16=-15,
故选:A.
点评 本题主要考查了根与系数的关系及根的判别式,属于中档题,关键要掌握x1,x2是方程x2+px+q=0的两根时,x1+x2=-p,x1x2=q.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案
相关题目
10.下列计算正确的是( )
| A. | m3+m3=m6 | B. | m3•m2=m6 | C. | (m3)2=m5 | D. | m3÷m2=m |
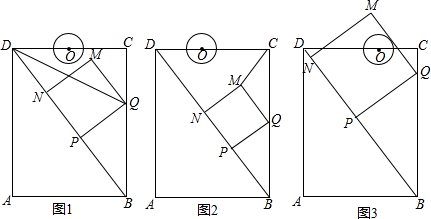
 在△ABC中,∠B=45°,∠C=30°,点D是BC上一点,连接AD,过点A作AG⊥AD,在AG上取点F,连接DF.延长DA至E,使AE=AF,连接EG,DG,且GE=DF.
在△ABC中,∠B=45°,∠C=30°,点D是BC上一点,连接AD,过点A作AG⊥AD,在AG上取点F,连接DF.延长DA至E,使AE=AF,连接EG,DG,且GE=DF.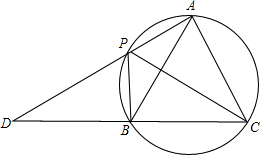 如图,A,P,B,C是圆上的四个点,∠APC=∠CPB=60°,AP,CB的延长线相交于点D.
如图,A,P,B,C是圆上的四个点,∠APC=∠CPB=60°,AP,CB的延长线相交于点D. 如图,已知BD是△ABC的角平分线,点E、F分别在边AB、BC上,ED∥BC,EF∥AC.求证:BE=CF.
如图,已知BD是△ABC的角平分线,点E、F分别在边AB、BC上,ED∥BC,EF∥AC.求证:BE=CF.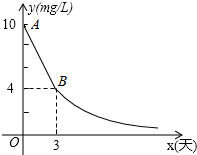 环保局对某企业排污情况进行检测,结果显示:所排污水中硫化物的浓度超标,即硫化物的浓度超过最高允许的1.0mg/L.环保局要求该企业立即整改,在15天以内(含15天)排污达标.整改过程中,所排污水中硫化物的浓度y(mg/L)与时间x(天)的变化规律如图所示,其中线段AB表示前3天的变化规律,从第3天起,所排污水中硫化物的浓度y与时间x成反比例关系.
环保局对某企业排污情况进行检测,结果显示:所排污水中硫化物的浓度超标,即硫化物的浓度超过最高允许的1.0mg/L.环保局要求该企业立即整改,在15天以内(含15天)排污达标.整改过程中,所排污水中硫化物的浓度y(mg/L)与时间x(天)的变化规律如图所示,其中线段AB表示前3天的变化规律,从第3天起,所排污水中硫化物的浓度y与时间x成反比例关系.