题目内容
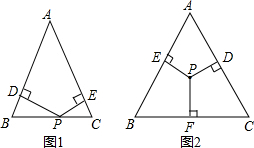 (1)如图1,在等腰△ABC中.AB=AC=a,面积是S,点P在BC上移动,过点P作PD⊥AB于点D,PE⊥AC于点E,那么点P到两腰的距离PD+PE等于什么?证明你的结论.
(1)如图1,在等腰△ABC中.AB=AC=a,面积是S,点P在BC上移动,过点P作PD⊥AB于点D,PE⊥AC于点E,那么点P到两腰的距离PD+PE等于什么?证明你的结论.(2)如图2,在等边△ABC中,边长是a,面积是S,点P是△ABC内部一点,P到三边的距离之和又等于什么?证明你的结论.
考点:等边三角形的性质,等腰三角形的性质
专题:探究型
分析:(1)连接AP,将三角形ABC的面积分成两个三角形的面积,即可得出答案;
(2)连接AP、BP、CP,将三角形ABC的面积分成三个三角形的面积,即可得出答案.
(2)连接AP、BP、CP,将三角形ABC的面积分成三个三角形的面积,即可得出答案.
解答: 解:(1)连接AP,
解:(1)连接AP,
∵S△ABC=S△ABP+S△CAP,
∴S△ABC=
+
,
∵AB=AC=a,S△ABC=S,
∴S=
,
∴PD+PE=
;
(2)连接AP、BP、CP,
∵S△ABC=S△ABP+S△CAP+S△CBP,
∴S△ABC=
+
+
,
∵AB=AC=BC=a,S△ABC=S,
∴S=
∴PD+PE+PF=
.
 解:(1)连接AP,
解:(1)连接AP,∵S△ABC=S△ABP+S△CAP,
∴S△ABC=
| AB•DP |
| 2 |
| AC•PE |
| 2 |
∵AB=AC=a,S△ABC=S,
∴S=
| a(PD+PE) |
| 2 |
∴PD+PE=
| 2S |
| a |
(2)连接AP、BP、CP,
∵S△ABC=S△ABP+S△CAP+S△CBP,
∴S△ABC=
| AB•PE |
| 2 |
| AC•PD |
| 2 |
| BC•PF |
| 2 |
∵AB=AC=BC=a,S△ABC=S,
∴S=
| a(PE+PD+PF) |
| 2 |
∴PD+PE+PF=
| 2S |
| a |
点评:本题考查了等腰三角形的性质、等边三角形的性质,是基础题,要掌握面积的计算公式.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
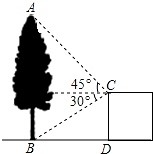 如图,在建筑平台CD的顶部C处,测得大树AB的顶部A的仰角为45°,测得大树AB的底部B的俯角为30°,已知平台CD的高度为5m,则大树的高度为
如图,在建筑平台CD的顶部C处,测得大树AB的顶部A的仰角为45°,测得大树AB的底部B的俯角为30°,已知平台CD的高度为5m,则大树的高度为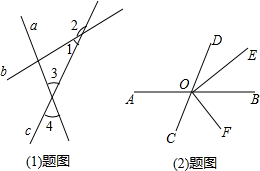 (1)如图,直线a,b,c两两相交,∠3=2∠1,∠2=155°,求∠4的度数.
(1)如图,直线a,b,c两两相交,∠3=2∠1,∠2=155°,求∠4的度数.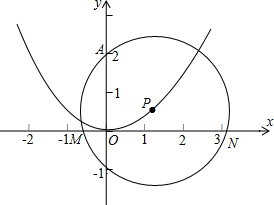 如图,抛物线y=ax2+bx+c(a,b,c是常数,a≠0)的对称轴为y轴,且经过(0,0)和(
如图,抛物线y=ax2+bx+c(a,b,c是常数,a≠0)的对称轴为y轴,且经过(0,0)和(