题目内容
已知抛物线y=x2+mx+n经过点(2,-1),且与x轴交于两点A(a,0)B(b,0),若点P为该抛物线的顶点,求使△PAB面积最小时抛物线的解析式.
考点:二次函数综合题
专题:计算题
分析:A、B两点在x轴上,用|AB|=|a-b|表示线段AB的长,由两根关系转化为m、n的表达式,根据顶点坐标公式得P(-
,
),故有S△APB=
|AB|•|
|,将点(2,-1)代入解析式得4+2m+n=-1,即n=-2m-5,转化为关于p的二次函数,求面积最小时m、n的值.
| m |
| 2 |
| 4n-m2 |
| 4 |
| 1 |
| 2 |
| 4n-m2 |
| 4 |
解答:解:由题意知4+2m+n=-1,即n=-2m-5,
∵A(a,0)、B(b,0)两点在抛物线y=x2+mx+n上,
∴a+b=-m,ab=n,
又∵|AB|=|a-b|=x2+mx+n经过(2,-1),代入得,n=-2m-5,
∴|AB|=
,P点纵坐标为-
m2-2m-5,
S△PAB=
=
,
可见,当m=-4时S△PAB最小,
解析式为y=x2-4x+3.
∵A(a,0)、B(b,0)两点在抛物线y=x2+mx+n上,
∴a+b=-m,ab=n,
又∵|AB|=|a-b|=x2+mx+n经过(2,-1),代入得,n=-2m-5,
∴|AB|=
| m2+8m+20 |
| 1 |
| 4 |
S△PAB=
| 1 |
| 4 |
| (m2+8m+20)3 |
| 1 |
| 4 |
| [(m+4)2+4]3 |
可见,当m=-4时S△PAB最小,
解析式为y=x2-4x+3.
点评:本题考查了抛物线与x轴的交点与顶点构成的三角形的面积问题,将原题转化为二次函数最值问题是解答的基本思路.

练习册系列答案
相关题目
若x2+3x-1=0,则x2+
的值为( )
| 1 |
| x2 |
| A、4 | B、7 | C、11 | D、-4 |
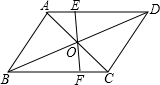 如图,O为平行四边形ABCD对角线AC、BD的交点,EF经过点O,且与边AD、BC分别交于点E、F,若BF=DE,则图中的全等三角形最多有( )
如图,O为平行四边形ABCD对角线AC、BD的交点,EF经过点O,且与边AD、BC分别交于点E、F,若BF=DE,则图中的全等三角形最多有( )