题目内容
若正六边形的半径是1,则正六边形的边长是 ;边心距是 ;面积是 .
考点:正多边形和圆
专题:
分析:先根据题意画出图形,再根据正六边形的性质求出∠BOC的度数,判断出△BOC为等边三角形即可求出答案.
解答: 解:如图所示,连接OB、OC;
解:如图所示,连接OB、OC;
∵此六边形是正六边形,
∴∠BOC=
=60°,
∵OB=OC=1,
∴△BOC是等边三角形,
∴OB=OC=BC=1.
作OM⊥BC于M点,
∴∠BOM=
∠BOC=30°,
∴
=cos30°,
即:边心距OM=cos30°OB=
∴正六边形的面积=
×6×
=
.
故答案为:1,
,
.
 解:如图所示,连接OB、OC;
解:如图所示,连接OB、OC;∵此六边形是正六边形,
∴∠BOC=
| 360° |
| 6 |
∵OB=OC=1,
∴△BOC是等边三角形,
∴OB=OC=BC=1.
作OM⊥BC于M点,
∴∠BOM=
| 1 |
| 2 |
∴
| OM |
| BC |
即:边心距OM=cos30°OB=
| ||
| 2 |
∴正六边形的面积=
| 1 |
| 2 |
| ||
| 2 |
3
| ||
| 2 |
故答案为:1,
| ||
| 2 |
3
| ||
| 2 |
点评:本题考查了正多边形与圆的知识,解答此题的关键是根据题意画出图形,作出辅助线;由正六边形的性质判断出△BOC的形状是解答此题的关键.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
已知|a|>a,|b|>b,且|a|>|b|,则a、b的大小关系为( )
| A、a>b | B、a=b |
| C、a<b | D、无法确定 |
任意抛掷一枚均匀的骰子两次,当骰子停止运动后朝上一面的数分别记为a,b,则关于x、y的方程组
有正整数解的概率为( )
|
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,半径为2的⊙O与正方形ABCD相切于点P、Q,弦MN=2,且MN在正方形的对角线BD上,则正方形的边长为
如图,半径为2的⊙O与正方形ABCD相切于点P、Q,弦MN=2,且MN在正方形的对角线BD上,则正方形的边长为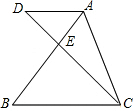 如图,线段AC、BD相交于E,AD∥BC,若AE:EB=1:2,且S△ADE=1,则△EBC的面积等于
如图,线段AC、BD相交于E,AD∥BC,若AE:EB=1:2,且S△ADE=1,则△EBC的面积等于



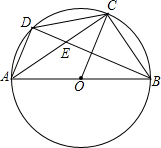 如图,已知△ABC内接于圆O,AB是直径,D是AC弧上的点,BD交AC于E,AB=5,sin∠CAB=
如图,已知△ABC内接于圆O,AB是直径,D是AC弧上的点,BD交AC于E,AB=5,sin∠CAB=