题目内容
2. 如图,四边形ABCD中,AD=CD,AB=BC,AC与BD交于点O.我们把这种两组邻边分别相等的四边形叫做“筝形”.请你猜想筝形的两条对角线AC与BD之间的位置关系,并证明你的结论.
如图,四边形ABCD中,AD=CD,AB=BC,AC与BD交于点O.我们把这种两组邻边分别相等的四边形叫做“筝形”.请你猜想筝形的两条对角线AC与BD之间的位置关系,并证明你的结论.
分析 根据SSS推出△DAB≌△DCB,根据全等三角形的性质得出∠ADB=∠CDB,根据等腰三角形的性质得出即可.
解答 AC⊥BD,
证明:∵在△DAB和△DCB中
$\left\{\begin{array}{l}{AD=CD}\\{BD=BD}\\{AB=CB}\end{array}\right.$
∴△DAB≌△DCB(SSS),
∴∠ADB=∠CDB,
∵AD=DC,
∴AC⊥BD.
点评 本题考查了等腰三角形的性质和全等三角形的性质和判定等知识点,能求出△DAB≌△DCB是解此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.计算:(1)$\frac{3}{4}\sqrt{3\frac{3}{4}}×(-18\sqrt{45})$;(2)$\sqrt{2x-3y}•\sqrt{4{x}^{2}-9{y}^{2}}$.
14.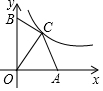 如图,在平面直角坐标系中,点A,B分别在x轴、y轴的正半轴上,OA=6,OB=9,点C在函数y=$\frac{k}{x}$(x>0)的图象上,当点C的横坐标为4时,△OAC与△OBC的面积相等,k的值为( )
如图,在平面直角坐标系中,点A,B分别在x轴、y轴的正半轴上,OA=6,OB=9,点C在函数y=$\frac{k}{x}$(x>0)的图象上,当点C的横坐标为4时,△OAC与△OBC的面积相等,k的值为( )
 如图,在平面直角坐标系中,点A,B分别在x轴、y轴的正半轴上,OA=6,OB=9,点C在函数y=$\frac{k}{x}$(x>0)的图象上,当点C的横坐标为4时,△OAC与△OBC的面积相等,k的值为( )
如图,在平面直角坐标系中,点A,B分别在x轴、y轴的正半轴上,OA=6,OB=9,点C在函数y=$\frac{k}{x}$(x>0)的图象上,当点C的横坐标为4时,△OAC与△OBC的面积相等,k的值为( )| A. | 16 | B. | 24 | C. | 30 | D. | 36 |
11.小派同学想给数学老师送张生日贺卡,但他只知道老师的生日在10月,那么他一次猜中老师生日的概率是( )
| A. | $\frac{1}{28}$ | B. | $\frac{1}{29}$ | C. | $\frac{1}{30}$ | D. | $\frac{1}{31}$ |
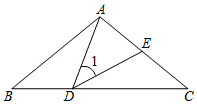 如图,△ABC中,AB=AC=5cm,∠BAC=100°,点D在线段BC上运动(不与点B、C重合),连接AD,作∠1=∠C,DE交线段AC于点E.
如图,△ABC中,AB=AC=5cm,∠BAC=100°,点D在线段BC上运动(不与点B、C重合),连接AD,作∠1=∠C,DE交线段AC于点E.
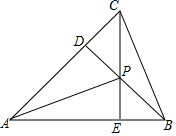 如图,△ABC的两条高BD、CE相交于点P,且PD=PE.求证:AC=AB.
如图,△ABC的两条高BD、CE相交于点P,且PD=PE.求证:AC=AB.