题目内容
12.已知一次函数y=kx+1是y随x的增大而减小的函敖,那么这个函数的图象与反比例函数$\frac{k}{x}$的图象的交点所在象限是二、四象限.分析 由题意可知:k<0,联立一次函数与反比例函数即可求出△>0,从而可知有两个交点,利用根与系数的关系即可求出交点的位置.
解答 解:由题意可知:k<0,
联立$\left\{\begin{array}{l}{y=\frac{k}{x}}\\{y=kx+1}\end{array}\right.$,
化简可得:kx2+x-k=0,
∵△=1+4k2>0,
∴一次函数与反比例函数由两个交点,
设这两个交点的横坐标分别为m、n,
∴mn=-1,m+n=-$\frac{1}{k}$
∴m与n的值必定是一正一负,
∴交点在第二、四象限
故答案为:二、四
点评 本题考查反比例函数与一次函数的交点问题,解题的关键是联立方程组化简得出kx2+x-k=0,本题属于中等题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.近年来,我国持续大面积的雾霾天气让环境和健康问题称为社会关注的焦点,为了调查学生对雾霾天气知识的了解程度,某校在学生中做了一次抽样调查,调查结果共分为四个等级:A非常了解B.比较了解;C.基本了解;D.不了解.根据调查统计结果,绘制了如图所示的不完整的三种统计图表.
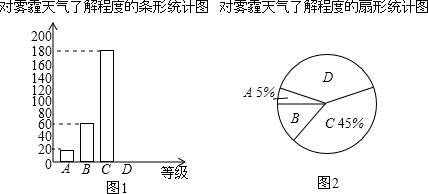
对雾霾所了解程度的统计表:
请结合统计图表,回答下列问题:
(1)求出本次参与调查的学生人数;
(2)请补全条形统计图;
(3)若该校共有2700名学生,根据抽样调查的结果,估计全校调查结果的等级为D的学生共有多少名?

对雾霾所了解程度的统计表:
| 对雾霾的了解程度 | 百分比 |
| A.非常了解 | 5% |
| A.比较了解 | 15% |
| C.基本了解 | 45% |
| D.不了解 | n |
(1)求出本次参与调查的学生人数;
(2)请补全条形统计图;
(3)若该校共有2700名学生,根据抽样调查的结果,估计全校调查结果的等级为D的学生共有多少名?
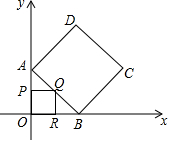 如图,在直角坐标系中,已知A(0,4)、B(4,0),以AB为边在第一象限内作正方形ABCD,在三角形AOB内部做正方形OPQR,使P、R、Q三点分别在线段OA、OB、AB上,将正方形OPQR绕点O顺时针旋转时,求点C到点Q距离的最大值与最小值.
如图,在直角坐标系中,已知A(0,4)、B(4,0),以AB为边在第一象限内作正方形ABCD,在三角形AOB内部做正方形OPQR,使P、R、Q三点分别在线段OA、OB、AB上,将正方形OPQR绕点O顺时针旋转时,求点C到点Q距离的最大值与最小值.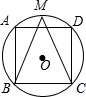 如图,正方形ABCD内接于⊙O,M为$\widehat{AD}$中点,连接BM,CM
如图,正方形ABCD内接于⊙O,M为$\widehat{AD}$中点,连接BM,CM 如图,∠1=70°,∠2=70°.说明:AB∥CD.
如图,∠1=70°,∠2=70°.说明:AB∥CD.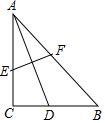 如图,在Rt△ABC中,∠C=90°,AC=BC,AD是BC边上的中线,将A点翻折与点D重合,得到折痕EF,则$\frac{CE}{AE}$=$\frac{3}{5}$.
如图,在Rt△ABC中,∠C=90°,AC=BC,AD是BC边上的中线,将A点翻折与点D重合,得到折痕EF,则$\frac{CE}{AE}$=$\frac{3}{5}$.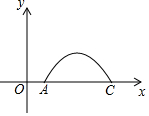 如图,一大桥有一段抛物线型的拱粱,小王骑自行车从O匀速沿直线到拱粱一端A,再匀速通过拱粱部分的桥面AC,小王从O到A用了3秒,当小王骑自行车行驶10秒时和20秒时拱粱的高度相同,则小王骑自行车通过拱粱部分的桥面AC共需24秒.
如图,一大桥有一段抛物线型的拱粱,小王骑自行车从O匀速沿直线到拱粱一端A,再匀速通过拱粱部分的桥面AC,小王从O到A用了3秒,当小王骑自行车行驶10秒时和20秒时拱粱的高度相同,则小王骑自行车通过拱粱部分的桥面AC共需24秒.