题目内容
6．
如图，PA是⊙O的切线，切点为A，PA=$\sqrt{3}$，∠APO=30°，则⊙O的半径为1．
分析 首先连接OA，由PA是⊙O的切线，可得∠PAO=90°，然后由PA=$\sqrt{3}$，∠APO=30°，直接利用三角函数的知识求解即可求得答案．
解答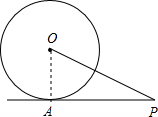 
解：连接OA，
∵PA是⊙O的切线，
∴∠PAO=90°，
∵PA=$\sqrt{3}$，∠APO=30°，
∴OA=PA•tan30°=$\sqrt{3}$×$\frac{\sqrt{3}}{3}$=1．
故答案为：1．
点评 此题考查了切线的性质．注意准确作出辅助线是解此题的关键．
练习册系列答案
相关题目
16．实验中学八年级（1）班50名学生参加期末考试，全班学生的数学成绩统计如表：
请根据表中提供的信息解答下列问题：
（1）该班学生这次考试数学成绩的众数是88分；
（2）该班学生这次考试数学成绩的中位数是86分；
（3）该班张华同学在这次考试中的数学成绩是83分，能不能说张华同学的数学成绩处于全班中游偏上水平？试说明理由．
| 成绩（分） | 71 | 74 | 78 | 80 | 82 | 83 | 85 | 86 | 88 | 90 | 91 | 92 | 94 |
| 人数 | 1 | 2 | 3 | 5 | 4 | 5 | 3 | 7 | 8 | 4 | 3 | 3 | 2 |
（1）该班学生这次考试数学成绩的众数是88分；
（2）该班学生这次考试数学成绩的中位数是86分；
（3）该班张华同学在这次考试中的数学成绩是83分，能不能说张华同学的数学成绩处于全班中游偏上水平？试说明理由．
17．某班体育委员记录了第一小组七位同学定点投篮（每人投10个）的情况，投进篮框的个数为6，10，5，3，4，8，4，这组数据的众数和极差分别是（ ）
| A． | 5，7 | B． | 7，5 | C． | 4，7 | D． | 3，7 |
14．下列各图中，描述∠1与∠2互为余角关系最准确的是（ ）
| A． |  | B． |  | C． |  | D． |  |
1．绝对值最小的有理数是（ ）
| A． | -1 | B． | 0 | C． | 1 | D． | 不存在 |
如图，如果曲线l1是反比例函数y=$\frac{k}{x}$在第一象限内的图象，且过点A（2，1），那么l1关于x轴对称的曲线l2的解析式为y=-$\frac{2}{x}$．
在一条直线上依次有A、B、C三个港口，甲、乙两船同时分别从A、B港口出发，沿直线匀速驶向C港，最终达到C港．设甲、乙两船行驶x（h）后，与B港的距离分别为y1、y2（km），y1、y2与x的函数关系如图所示．