题目内容
6.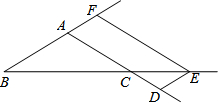 在△ABC中,AD=BF,点D,E,F分别是AC,BC,BA延长线上的点,四边形ADEF为平行四边形.
在△ABC中,AD=BF,点D,E,F分别是AC,BC,BA延长线上的点,四边形ADEF为平行四边形.求证:AB=AC.
分析 根据平行四边形的对边平行且相等可得AD=EF,AD∥EF,再根据两直线平行,同位角相等可得∠2=∠3,根据等边对等角求出∠1=∠3,从而得到∠1=∠2,然后根据等角对等边证明即可.
解答 证明:∵四边形ADEF是平行四边形,
∴AD=EF AD∥EF,
∴∠2=∠3,
又∵AD=BF,
∴BF=EF,
∴∠1=∠3,
∴∠1=∠2,
∴AB=AC.
点评 本题考查了平行四边形对边平行且相等的性质,平行线的性质,等角对等边的性质,熟练掌握各性质是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.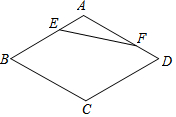 如图,在菱形ABCD中,∠B=60°,AB=a,点E,F分别是边AB,AD上的动点,且AE+AF=a,则线段EF的最小值为( )
如图,在菱形ABCD中,∠B=60°,AB=a,点E,F分别是边AB,AD上的动点,且AE+AF=a,则线段EF的最小值为( )
 如图,在菱形ABCD中,∠B=60°,AB=a,点E,F分别是边AB,AD上的动点,且AE+AF=a,则线段EF的最小值为( )
如图,在菱形ABCD中,∠B=60°,AB=a,点E,F分别是边AB,AD上的动点,且AE+AF=a,则线段EF的最小值为( )| A. | 2$\sqrt{3}$a | B. | $\frac{\sqrt{3}}{2}$a | C. | $\sqrt{3}$a | D. | $\frac{a}{2}$ |
 如图,平面直角坐标系xOy中,正方形一的顶点坐标分别为A(1,3),B(1,1),C(3,1),D(3,3).直线y=kx+b(k≠0)经过点P(-2,0),则$\frac{k}{b}$=$\frac{1}{2}$;若直线y=kx+b在绕点P旋转的过程中,同时与AB边、CD边有公共点,则b的取值范围是$\frac{2}{3}$<b<$\frac{6}{5}$.
如图,平面直角坐标系xOy中,正方形一的顶点坐标分别为A(1,3),B(1,1),C(3,1),D(3,3).直线y=kx+b(k≠0)经过点P(-2,0),则$\frac{k}{b}$=$\frac{1}{2}$;若直线y=kx+b在绕点P旋转的过程中,同时与AB边、CD边有公共点,则b的取值范围是$\frac{2}{3}$<b<$\frac{6}{5}$.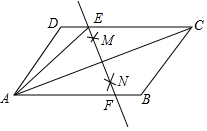 在平行四边形ABCD中,连接AC,按以下步骤作图,分别以A、C为圆心,以大于$\frac{1}{2}$AC的长为半径画弧,两弧分别相交于点M、N,作直线MN交CD于点E,交AB于点F.若AB=6,BC=4,则△ADE的周长为10.
在平行四边形ABCD中,连接AC,按以下步骤作图,分别以A、C为圆心,以大于$\frac{1}{2}$AC的长为半径画弧,两弧分别相交于点M、N,作直线MN交CD于点E,交AB于点F.若AB=6,BC=4,则△ADE的周长为10.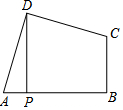 如图,在面积为16的四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于点P,则DP的长是4.
如图,在面积为16的四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于点P,则DP的长是4. 如图,在平行四边形ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,大于$\frac{1}{2}BF$长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF.
如图,在平行四边形ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,大于$\frac{1}{2}BF$长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF. 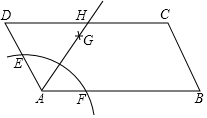 如图,在平行四边形ABCD中,以点A为圆心,一定长为半径作圆弧,分别交AD、AB于点E、F;再分别以点E、F为圆心,大于$\frac{1}{2}$EF的长为半径作弧,两弧交于点G;作射线AG,交边CD于点H.若AB=6,AD=4,则四边形ABCH的周长与三角形ADH的周长之差为( )
如图,在平行四边形ABCD中,以点A为圆心,一定长为半径作圆弧,分别交AD、AB于点E、F;再分别以点E、F为圆心,大于$\frac{1}{2}$EF的长为半径作弧,两弧交于点G;作射线AG,交边CD于点H.若AB=6,AD=4,则四边形ABCH的周长与三角形ADH的周长之差为( )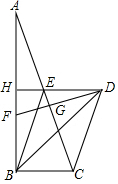 如图,在Rt△ABC中,∠ABC=90°,DH垂直平分AB交AC于点E,连接BE、CD,CD=CE,点F在AB上,BF=BC,连接BD,BD平分∠ABC.
如图,在Rt△ABC中,∠ABC=90°,DH垂直平分AB交AC于点E,连接BE、CD,CD=CE,点F在AB上,BF=BC,连接BD,BD平分∠ABC.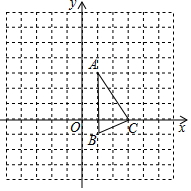 如图,△ABC位于直角坐标系内,且三个顶点均在正方形的网格的顶点上.
如图,△ABC位于直角坐标系内,且三个顶点均在正方形的网格的顶点上.