题目内容
16.(1)-22×2$\frac{1}{4}$+(-3)3×(-$\frac{8}{27}$)(2)$\frac{x+3}{6}$=1-$\frac{3-2x}{4}$.
分析 (1)原式先计算乘方运算,再计算乘法运算,最后算加减运算即可得到结果;
(2)方程去分母,去括号,移项合并,把x系数化为1,即可求出解.
解答 解:(1)原式=-4×$\frac{9}{4}$-27×(-$\frac{8}{27}$)=-9+8=-1;
(2)去分母得:2(x+3)=12-3(3-2x),
去括号得:2x+6=12-9+6x,
移项合并得:-4x=-3,
解得:x=$\frac{3}{4}$.
点评 此题考查了解一元一次方程,以及有理数的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.若一次函数y=kx+b的函数值y随x的增大而增大,且图象与y轴的负半轴相交,那么k和b的符号正确的是( )
| A. | k>0,b>0 | B. | k<0,b<0 | C. | k<0,b>0 | D. | k>0,b>0 |
4.在课堂上,张老师布置了一道画图题:
画一个Rt△ABC,使∠B=90°,它的两条边分别等于两条已知线段.小刘和小赵同学先画出了∠MBN=90°之后,后续画图的主要过程分别如图所示.

那么小刘和小赵同学作图确定三角形的依据分别是( )
画一个Rt△ABC,使∠B=90°,它的两条边分别等于两条已知线段.小刘和小赵同学先画出了∠MBN=90°之后,后续画图的主要过程分别如图所示.

那么小刘和小赵同学作图确定三角形的依据分别是( )
| A. | SAS,HL | B. | HL,SAS | C. | SAS,AAS | D. | AAS,HL |
11.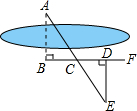 如图,要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使BC=CD,再作出BF的垂线DE,使点A、C、E在同一条直线上(如图所示),可以说明△ABC≌△EDC,得AB=DE,因此测得DE的长就是AB的长,判定△ABC≌△EDC,最恰当的理由是( )
如图,要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使BC=CD,再作出BF的垂线DE,使点A、C、E在同一条直线上(如图所示),可以说明△ABC≌△EDC,得AB=DE,因此测得DE的长就是AB的长,判定△ABC≌△EDC,最恰当的理由是( )
 如图,要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使BC=CD,再作出BF的垂线DE,使点A、C、E在同一条直线上(如图所示),可以说明△ABC≌△EDC,得AB=DE,因此测得DE的长就是AB的长,判定△ABC≌△EDC,最恰当的理由是( )
如图,要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使BC=CD,再作出BF的垂线DE,使点A、C、E在同一条直线上(如图所示),可以说明△ABC≌△EDC,得AB=DE,因此测得DE的长就是AB的长,判定△ABC≌△EDC,最恰当的理由是( )| A. | 边角边 | B. | 角边角 | C. | 边边边 | D. | 边边角 |
6.甲乙两辆汽车在一条公路上匀速行驶,为了确定汽车的位置,我们用数轴表示这条公路,并规定向右为正方向,原点O为0km路标.并作如下约定:位置为正,表示汽车位于零千米右侧;位置为负,表示汽车位于零千米左侧,位置为零,表示汽车位于零千米处.
(1)根据题意,填写下列表格:
(2)求出两车的相遇时间.
(1)根据题意,填写下列表格:
| 时间(h) | 0 | 3 | 5 | x |
| 甲车位置(km) | 150 | -30 | -150 | 150-60x |
| 乙车位置(km) | -50 | 70 | 150 | -50+40x |
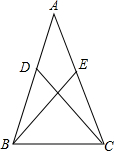 如图,在△ABC中,点D、点E分别在AB、AC上,连接BE、CD,现有下列三个式子:?①AB=AC,?②BD=CE,③?CD=BE.请从三个式子中选两个合适的式子作为已知条件,剩下的一个式子作为待说明成立的结论,并说明该结论的正确性.
如图,在△ABC中,点D、点E分别在AB、AC上,连接BE、CD,现有下列三个式子:?①AB=AC,?②BD=CE,③?CD=BE.请从三个式子中选两个合适的式子作为已知条件,剩下的一个式子作为待说明成立的结论,并说明该结论的正确性. 已知:在平行四边形ABCD中,O是对角线BD的中点,P为线段BC上一点,连接PO并延长交AD于点Q,求证:OP=OQ.
已知:在平行四边形ABCD中,O是对角线BD的中点,P为线段BC上一点,连接PO并延长交AD于点Q,求证:OP=OQ.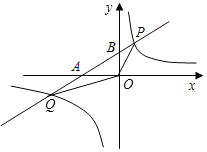 如图,已知反比例函数的图象与一次函数y=kx+1的图象相交于P、Q两点,直线y=kx+1分别与x轴,y轴交于A、B两点,∠BOP=45°,tan∠BAO=$\frac{1}{2}$.
如图,已知反比例函数的图象与一次函数y=kx+1的图象相交于P、Q两点,直线y=kx+1分别与x轴,y轴交于A、B两点,∠BOP=45°,tan∠BAO=$\frac{1}{2}$.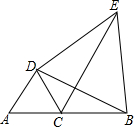 如图,点C在线段AB上,△DAC和△DBE都是等边三角形,试说明:△DAB≌△DCE.
如图,点C在线段AB上,△DAC和△DBE都是等边三角形,试说明:△DAB≌△DCE.