题目内容
11.已知关于x的方程x2-mx+m-2=0的两个根为x1、x2,则x1+x2-x1x2=2.分析 利用根与系数的关系求出两根之和与两根之积,代入所求式子中计算即可求出值.
解答 解:∵x1,x2是方程x2-mx+m-2=0的两根,
∴x1+x2=m,x1•x2=m-2,
则x1+x2-x1•x2=m-(m-2)=2.
故答案为2.
点评 此题考查了一元二次方程根与系数的关系,熟练掌握根与系数的关系是解本题的关键.

练习册系列答案
相关题目
2. 如图,已知直线AC∥ED,∠C=30°,∠BED=70°,则∠CBE度数是( )
如图,已知直线AC∥ED,∠C=30°,∠BED=70°,则∠CBE度数是( )
 如图,已知直线AC∥ED,∠C=30°,∠BED=70°,则∠CBE度数是( )
如图,已知直线AC∥ED,∠C=30°,∠BED=70°,则∠CBE度数是( )| A. | 20° | B. | 100° | C. | 55° | D. | 40° |
6.在?ABCD中,AB=3,BC=4,当?ABCD的面积最大时,下列结论正确的有( )
①AC=5;②∠A+∠C=180°;③AC⊥BD;④AC=BD.
①AC=5;②∠A+∠C=180°;③AC⊥BD;④AC=BD.
| A. | ①②③ | B. | ①②④ | C. | ②③④ | D. | ①③④ |
16.sin30°的值等于( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
1.下列运算正确的是( )
| A. | x3•x2=x6 | B. | $({x^2}{)^{\frac{1}{2}}}=x$ | C. | x0=1 | D. | x5÷x3=x2 |
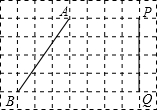 如图,方格纸中每个小正方形的边长均为1,线段AB和PQ的端点均在小正方形的顶点上.
如图,方格纸中每个小正方形的边长均为1,线段AB和PQ的端点均在小正方形的顶点上.
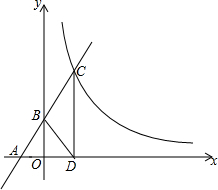 如图,在直角坐标系xOy中,一直线y=2x+b经过点A(-1,0)与y轴正半轴交于B点,在x轴正半轴上有一点D,且OB=OD,过D点作DC⊥x轴交直线y=2x+b于C点,反比例函数y=$\frac{k}{x}$(x>0)经过点C.
如图,在直角坐标系xOy中,一直线y=2x+b经过点A(-1,0)与y轴正半轴交于B点,在x轴正半轴上有一点D,且OB=OD,过D点作DC⊥x轴交直线y=2x+b于C点,反比例函数y=$\frac{k}{x}$(x>0)经过点C.