题目内容
6.在?ABCD中,AB=3,BC=4,当?ABCD的面积最大时,下列结论正确的有( )①AC=5;②∠A+∠C=180°;③AC⊥BD;④AC=BD.
| A. | ①②③ | B. | ①②④ | C. | ②③④ | D. | ①③④ |
分析 当?ABCD的面积最大时,四边形ABCD为矩形,得出∠A=∠B=∠C=∠D=90°,AC=BD,根据勾股定理求出AC,即可得出结论.
解答 解:根据题意得:当?ABCD的面积最大时,四边形ABCD为矩形,
∴∠A=∠B=∠C=∠D=90°,AC=BD,
∴AC=$\sqrt{{3}^{2}+{4}^{2}}$=5,
①正确,②正确,④正确;③不正确;
故选:B.
点评 本题考查了平行四边形的性质、矩形的性质以及勾股定理;得出?ABCD的面积最大时,四边形ABCD为矩形是解决问题的关键.

练习册系列答案
相关题目
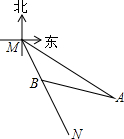 如图,已知射线MN表示一艘轮船的航线路线,从M到N的走向为南偏东30°,在M的南偏东60°方向上有一点A,A处到M处为80海里.
如图,已知射线MN表示一艘轮船的航线路线,从M到N的走向为南偏东30°,在M的南偏东60°方向上有一点A,A处到M处为80海里. 如图,在⊙O中,AB为⊙O的直径,C,D为⊙O的两点,若∠ADC=56°,则∠BAC=34°.
如图,在⊙O中,AB为⊙O的直径,C,D为⊙O的两点,若∠ADC=56°,则∠BAC=34°. 一个全透明的正方体上面嵌有一根黑色的金属丝,如图所示,金属丝在俯视图中的形状是( )
一个全透明的正方体上面嵌有一根黑色的金属丝,如图所示,金属丝在俯视图中的形状是( )


