题目内容
17.在等腰△ABC中,AB=AC,△ABC周长为16cm,AC边上的中线BD把△ABC分成周长差为4cm的两个三角形,求△ABC各边的长.分析 结合图形两腰长的差就是腰长与底边的差,因为腰长与底边的大小不明确,所以分腰长大于底边和腰长小于底边两种情况讨论.
解答 解:根据题意,分成两部分的周长的差等于腰长与底边的差,
(1)若AB>BC,则AB-BC=4,
又因为2AB+BC=16,
联立方程组得:$\left\{\begin{array}{l}{AB-BC=4}\\{2AB+BC=16}\end{array}\right.$,
解得:AB=$\frac{20}{3}$,BC=$\frac{8}{3}$,
$\frac{20}{3}$cm、$\frac{20}{3}$cm、$\frac{8}{3}$cm三边能够组成三角形;
(2)若AB<BC,则BC-AB=4,
又因为2AB+BC=16,
联立方程组得:$\left\{\begin{array}{l}{BC-AB=4}\\{2AB+BC=16}\end{array}\right.$,
解得:AB=4,BC=8,
4cm、4cm、8cm三边不能够组成三角形;
因此三角形的各边长为$\frac{20}{3}$cm、$\frac{20}{3}$cm、$\frac{8}{3}$cm.
点评 本题主要考查等腰三角形的性质及三角形三边关系;做题中利用了分类讨论的思想,注意运用三角形三边关系对三角形的组成情况作出判断,这是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.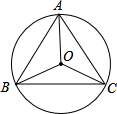 如图是一个旋转对称图形,以O为旋转中心,以下列哪一个角为旋转角旋转,能使旋转后的图形与原图形重合( )
如图是一个旋转对称图形,以O为旋转中心,以下列哪一个角为旋转角旋转,能使旋转后的图形与原图形重合( )
 如图是一个旋转对称图形,以O为旋转中心,以下列哪一个角为旋转角旋转,能使旋转后的图形与原图形重合( )
如图是一个旋转对称图形,以O为旋转中心,以下列哪一个角为旋转角旋转,能使旋转后的图形与原图形重合( )| A. | 60° | B. | 150° | C. | 180° | D. | 240° |
 如图,∠α=105°.
如图,∠α=105°.