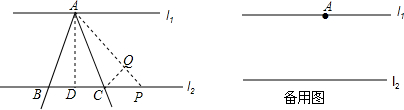如图所示.则∠A+∠B+∠C+∠D+∠E+∠F的度数是( )A．180°B．270°C．360°D．540° 题目和参考答案——青夏教育精英家教网—

题目内容

9．

如图所示，则∠A+∠B+∠C+∠D+∠E+∠F的度数是（　　）

A．

180°

B．

270°

C．

360°

D．

540°

分析根据三角形外角的性质，可得∠1与∠E、∠F的关系，∠1、∠2、∠D的关系，根据多边形的内角和公式，可得答案．

解答解：如图延长AF交DC于G点，

由三角形的外角等于与它不相邻的两个内角的和，得
∠1=∠E+∠F，∠2=∠1+∠D，
由等量代换，得∠2=∠E+∠F+∠D，
∠A+∠B+∠C+∠D+∠E+∠F=∠A+∠B+∠2+∠C=（4-2）×180°=360°．
故选：C．

点评本题考查的是三角形外角的性质及三角形的外角和，熟知三角形的外角和是360度是解答此题的关键．

练习册系列答案

17．若菱形的两条对角线长分别是6和8，则此菱形的周长是20，面积是24．

4．如图，已知直线l₁∥l₂，一个45°角的顶点A在l₁上，过A作AD⊥l₂，垂足为D，AD=6．将这个角绕顶点A旋转（角的两边足够长）．
（1）如图，旋转过程中，若角的两边与l₂分别交于B、C，且AB=AC，求BD的长．为了解决这个问题，下面提供一种解题思路：如图，作∠DAP=45°，AP与l₂相交于点P，过点C作CQ⊥AP于点Q．∵∠DAP=∠BAC=45°，∴∠BAD=∠CAQ，请你接下去完成解答．
（2）旋转过程中，若角的两边与l₂分别交于E、F（E在F左面），且AE＞AF，DF=2，求DE的长．请你借鉴（1）的做法在备用图中画图并解答这个问题．

x²•x³=x³

（-x⁵）⁴=x²⁰

（a²）³=a⁵

1．如果单项式-3x^4a-by²与$\frac{1}{3}$x³y^a+b是同类项，那么这两个单项式的积是-x⁶y⁴．

18．计算：
（1）$\sqrt{32}$-$\sqrt{\frac{1}{8}}$+$\frac{1}{5}$$\sqrt{75}-3\sqrt{\frac{1}{3}}$+4$\sqrt{\frac{1}{2}}$
（2）a²$\sqrt{18a}+3a\sqrt{50{a}^{3}}-\frac{a}{2}\sqrt{32{a}^{3}}$．

19．求代数式4a（3a-b）+（a+2b）（a-2b）-（3a-b）²的值，其中a、b满足3^a=27=b³．

试题分类