题目内容
19.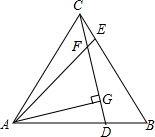 如图,等边三角形ABC中,DE分别是AB,BC边上的点,AD=BE,AE与CD相交于F,AG⊥CD,垂足为G,则sin∠AFG=$\frac{\sqrt{3}}{2}$.
如图,等边三角形ABC中,DE分别是AB,BC边上的点,AD=BE,AE与CD相交于F,AG⊥CD,垂足为G,则sin∠AFG=$\frac{\sqrt{3}}{2}$.
分析 根据等边三角形的性质得到AB=BC,∠ACB=∠B=60°,由已知条件得到CE=BD,推出△ACE≌△CBD(SAS),根据全等三角形的性质得到∠AEC=∠CDB,由于∠BCD+∠AEC+∠CFE=180°,∠BCD+∠CDB+∠B=180°,于是得到∠CFE=∠B=60°,证得∠AFG=∠CFE=60°,即可得到结论.
解答 解:∵△ABC为等边三角形,
∴AB=BC,∠ACB=∠B=60°,
∵AD=BE,
∴CE=BD,
在△ACE和△CBD中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACB=∠B=60°}\\{CE=BD}\end{array}\right.$,
∴△ACE≌△CBD(SAS),
∴∠AEC=∠CDB,
∵∠BCD+∠AEC+∠CFE=180°,∠BCD+∠CDB+∠B=180°,
∴∠CFE=∠B=60°,
∴∠AFG=∠CFE=60°,
∴sin∠AFG=$\frac{\sqrt{3}}{2}$.
故答案为:$\frac{\sqrt{3}}{2}$.
点评 本题考查了全等三角形的判定,考查了全等三角形对应角相等的性质,本题中求证△ACE≌△CBD是解题的关键.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
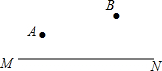 直线MN和同侧两点AB,在MN上找一点P,使得PA+PB最小.(尺规作图)
直线MN和同侧两点AB,在MN上找一点P,使得PA+PB最小.(尺规作图)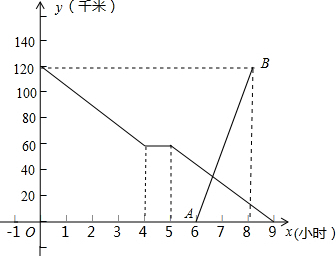 张老师骑自行车匀速从甲地到乙地,在途中休息了一段时间后,仍按原速行驶,他距乙地的距离与时间的关系如图中折线所示,李老师骑摩托车沿同一条路匀速从乙地到甲地,比张老师晚出发一段时间,他距乙地的距离与时间的关系如图中线段EF所示.
张老师骑自行车匀速从甲地到乙地,在途中休息了一段时间后,仍按原速行驶,他距乙地的距离与时间的关系如图中折线所示,李老师骑摩托车沿同一条路匀速从乙地到甲地,比张老师晚出发一段时间,他距乙地的距离与时间的关系如图中线段EF所示. 如图,在平面直角坐标系中,矩形ABCO的面积为15,OA比OC大2,点E为BC的中点,以OE为直径的⊙O′交x轴于点D,过D作DF⊥EA.交AE于点F.
如图,在平面直角坐标系中,矩形ABCO的面积为15,OA比OC大2,点E为BC的中点,以OE为直径的⊙O′交x轴于点D,过D作DF⊥EA.交AE于点F.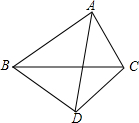 已知:如图,△ABC,BD=CD,AD平分∠BAC,求证:∠BAC+∠BDC=180°.
已知:如图,△ABC,BD=CD,AD平分∠BAC,求证:∠BAC+∠BDC=180°. 如图,E、F为线段AB的三等分点,P为线段AB上一动点(P不与E、F、A、B重合),在点P运动过程中,PE、PF、PA有何数量关系?请写出结论并说明理由.
如图,E、F为线段AB的三等分点,P为线段AB上一动点(P不与E、F、A、B重合),在点P运动过程中,PE、PF、PA有何数量关系?请写出结论并说明理由.