题目内容
8.解方程组:$\left\{\begin{array}{l}2x-y=-3\\ 3x+2y=13\end{array}\right.$.分析 先用加减消元法,再用代入消元法即可.
解答 解:$\left\{\begin{array}{l}{2x-y=-3①}\\{3x+2y=13②}\end{array}\right.$,
①×2,得4x-2y=-6 ③,
③+②,得7x=7,
∴x=1.
代入①,得2-y=-3,
∴y=5.
∴方程组的解为$\left\{\begin{array}{l}{x=1}\\{y=5}\end{array}\right.$.
点评 本题考查了解二元一次方程组,解题关键是掌握方程组解法中的加减消元法.

练习册系列答案
相关题目
3.以下计算正确的是( )
| A. | $\sqrt{2}+\sqrt{4}=\sqrt{6}$ | B. | $\root{3}{27}$=9 | C. | $\sqrt{{{(-3)}^2}}$=3 | D. | $(\sqrt{5}-\sqrt{2})(\sqrt{5}+\sqrt{2})$=10 |
13.已知∠AOB=50°,∠COB=30°,则∠AOC等于( )
| A. | 80° | B. | 20° | C. | 80°或20° | D. | 无法确定 |
17.下列计算正确的是( )
| A. | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{5}$ | B. | $\sqrt{27}$$÷\sqrt{3}$=9 | C. | $\sqrt{{4}^{2}+{3}^{2}}$=4+3=7 | D. | $\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}$ |
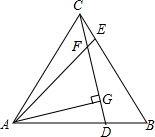 如图,等边三角形ABC中,DE分别是AB,BC边上的点,AD=BE,AE与CD相交于F,AG⊥CD,垂足为G,则sin∠AFG=$\frac{\sqrt{3}}{2}$.
如图,等边三角形ABC中,DE分别是AB,BC边上的点,AD=BE,AE与CD相交于F,AG⊥CD,垂足为G,则sin∠AFG=$\frac{\sqrt{3}}{2}$.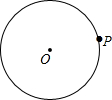 链球运动员在投掷链球时,链球按顺时针作圆周运动,如图,当运动员即将放手时,链球在⊙O的点P处.
链球运动员在投掷链球时,链球按顺时针作圆周运动,如图,当运动员即将放手时,链球在⊙O的点P处.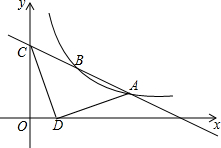 如图,已知一次函数y=k1x+b与反比例函数y=$\frac{{k}_{2}}{x}$的图象相交于A(4,1)、B(a,2)两点,一次函数的图象与y轴的交点为C.
如图,已知一次函数y=k1x+b与反比例函数y=$\frac{{k}_{2}}{x}$的图象相交于A(4,1)、B(a,2)两点,一次函数的图象与y轴的交点为C.