题目内容
 如图,将矩形ABCD沿AE折叠,点D恰好落在BC边上的点F处,如果AB:AD=2:3,那么cos∠EFC的值是
如图,将矩形ABCD沿AE折叠,点D恰好落在BC边上的点F处,如果AB:AD=2:3,那么cos∠EFC的值是考点:翻折变换(折叠问题)
专题:
分析:设出参数:AB=2μ,则AF=AD=3μ,EC=2μ-λ;求出BF=
μ,CF=3μ;进而求出λ=
μ,即可解决问题.
| 5 |
3(3-
| ||
| 2 |
解答: 解:如图,∵四边形ABCD为矩形,
解:如图,∵四边形ABCD为矩形,
∴BC=AD,DC=AB;∠B=∠C=90°;
由题意得:DE=EF(设为λ);
∵AB:AD=2:3,
∴设AB=2μ,则AF=AD=3μ,EC=2μ-λ;
由勾股定理得:BF2=9μ2-4μ2=5μ2,
∴BF=
μ,CF=3μ-
μ;
由勾股定理得:λ2=(3μ-
μ)2+(2μ-λ)2,
解得:λ=
μ,
∴cos∠EFC=
=
.
故答案为
.
 解:如图,∵四边形ABCD为矩形,
解:如图,∵四边形ABCD为矩形,∴BC=AD,DC=AB;∠B=∠C=90°;
由题意得:DE=EF(设为λ);
∵AB:AD=2:3,
∴设AB=2μ,则AF=AD=3μ,EC=2μ-λ;
由勾股定理得:BF2=9μ2-4μ2=5μ2,
∴BF=
| 5 |
| 5 |
由勾股定理得:λ2=(3μ-
| 5 |
解得:λ=
3(3-
| ||
| 2 |
∴cos∠EFC=
| CF |
| EF |
| 2 |
| 3 |
故答案为
| 2 |
| 3 |
点评:该题主要考查了矩形的性质、勾股定理等几何知识点的应用问题;灵活运用勾股定理等几何知识点来分析、判断、推理或解答是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
有2张边长为a的正方形纸片,6张边长为a,b的长方形纸片,10张边长为b的正方形纸片,从中取出若干张纸片,每种纸片至少取一张,把取出的这些纸片拼出一个大的正方形(无空隙,无重叠地拼接)则拼出的正方形的边长最长可以为( )
| A、a+3b | B、3a+b |
| C、2a+2b | D、2a+3b |
在△ABC中,AB=AC,那么在这个三角形中,三线重合的线段是( )
| A、∠A的平分线,AB边上的中线,AB边上的高 |
| B、∠A的平分线,BC边上的中线,BC边上的高 |
| C、∠B的平分线,AC边上的中线,AC边上的高 |
| D、∠C的平分线,AB边上的中线,AB边上的高 |
以下列各组数为边的三角形不是直角三角形的是( )
| A、5,6,9 |
| B、5,3,4 |
| C、24,10,26 |
| D、60,11,61 |
 如图,长方形ABCD中AD∥BC,边AB=4,BC=8.将此长方形沿EF折叠,使点D与点B重合,点C落在点G处.
如图,长方形ABCD中AD∥BC,边AB=4,BC=8.将此长方形沿EF折叠,使点D与点B重合,点C落在点G处.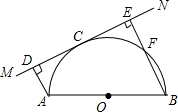 如图,已知AB为半圆O的直径,直线MN切半圆于点C,AD⊥MN于点D,BE⊥MN于点E,BE交半圆于点F,AD=3cm,BE=7cm.
如图,已知AB为半圆O的直径,直线MN切半圆于点C,AD⊥MN于点D,BE⊥MN于点E,BE交半圆于点F,AD=3cm,BE=7cm. 如图,在平面直角坐标系中,一颗,棋子从点P处开始依次关于点A,B,C作循环对称跳动,即第一次跳到点P关于点A的对称点M处,接着跳到点M关于点B的对称点N处,第三次再跳到点N关于点C的对称点处,…,如此下去.则经过第2013次跳动之后,棋子落点的坐标为
如图,在平面直角坐标系中,一颗,棋子从点P处开始依次关于点A,B,C作循环对称跳动,即第一次跳到点P关于点A的对称点M处,接着跳到点M关于点B的对称点N处,第三次再跳到点N关于点C的对称点处,…,如此下去.则经过第2013次跳动之后,棋子落点的坐标为