题目内容
19.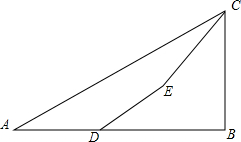 如图,为了测量某建筑物BC的高度,小明先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地而上向建筑物前进了50m到达D处,此时遇到一斜坡,坡度i=1:$\sqrt{3}$,沿着斜坡前进20米到达E处测得建筑物顶部的仰角是45°,(坡度i=1:$\sqrt{3}$是指坡面的铅直高度FE与水平宽度DE的比).请你计算出该建筑物BC的高度.(取$\sqrt{3}$=1.732,结果精确到0.1m).
如图,为了测量某建筑物BC的高度,小明先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地而上向建筑物前进了50m到达D处,此时遇到一斜坡,坡度i=1:$\sqrt{3}$,沿着斜坡前进20米到达E处测得建筑物顶部的仰角是45°,(坡度i=1:$\sqrt{3}$是指坡面的铅直高度FE与水平宽度DE的比).请你计算出该建筑物BC的高度.(取$\sqrt{3}$=1.732,结果精确到0.1m).
分析 过E作EF⊥AB于F,EG⊥BC与G,根据矩形的性质得到四边形EG=FB,EF=BG,设CG=x,根据已知条件得到∠EDF=30°及直角三角形得到DF=20cos30°=10$\sqrt{3}$,BG=EF=20sin30°=10,AB=50+10$\sqrt{3}$+x,BC=x+10,在Rt△ABC中,根据三角函数的定义列方程即可得到结论.
解答  解:过E作EF⊥AB于F,EG⊥BC与G,
解:过E作EF⊥AB于F,EG⊥BC与G,
∵CB⊥AB,
∴四边形EFBG是矩形,
∴EG=FB,EF=BG,
设CG=x米,
∵∠CEG=45°,
∴FB=EG=CG=x,
∵DE的坡度i=1:$\sqrt{3}$,
∴∠EDF=30°,
∵DE=20,
∴DF=20cos30°=10$\sqrt{3}$,BG=EF=20sin30°=10,
∴AB=50+10$\sqrt{3}$+x,BC=x+10,
在Rt△ABC中,
∵∠A=30°,
∴BC=AB•tan∠A,
即x+10=$\frac{\sqrt{3}}{3}$(50+10$\sqrt{3}$+x),
解得:x≈68.3,
∴BC=7.3米,
答:建筑物BC的高度是78.3米.
点评 本题考查了仰角与俯角的知识.此题难度适中,注意能借助仰角与俯角构造直角三角形并解直角三角形是解此题的关键,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
相关题目
9.下列各式中,正确的是( )
| A. | $\root{3}{-2}$=-$\root{3}{2}$ | B. | -$\sqrt{0.4}$=-0.2 | C. | $\sqrt{(-3)^{2}}$=-3 | D. | $\sqrt{9}$=±3 |
7.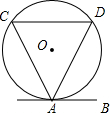 如图,直线AB与⊙O相切于点A,弦CD∥AB,若⊙O的半径为$\frac{5}{2}$,CD=4,则弦AD的长为( )
如图,直线AB与⊙O相切于点A,弦CD∥AB,若⊙O的半径为$\frac{5}{2}$,CD=4,则弦AD的长为( )
 如图,直线AB与⊙O相切于点A,弦CD∥AB,若⊙O的半径为$\frac{5}{2}$,CD=4,则弦AD的长为( )
如图,直线AB与⊙O相切于点A,弦CD∥AB,若⊙O的半径为$\frac{5}{2}$,CD=4,则弦AD的长为( )| A. | 4 | B. | 2$\sqrt{5}$ | C. | 5 | D. | 6 |
14.计算(-8)-(-5)的结果等于( )
| A. | -3 | B. | -13 | C. | -40 | D. | 3 |
11.(1)计算:($\frac{1}{3}$)-2-|1-$\sqrt{2}$|+(π-3.14)0+$\frac{1}{2}$$\sqrt{8}$+tan60°
(2)解方程:2x2-3x-3=0.
(2)解方程:2x2-3x-3=0.
8.甲箱内有4颗球,颜色分别为红、黄、绿、蓝;乙箱内有3颗球,颜色分别为红、黄、黑.小赖打算同时从甲、乙两个箱子中各抽出一颗球,若同一箱中每球被抽出的机会相等,则小赖抽出的两颗球颜色相同的机率为何?( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{6}$ | C. | $\frac{2}{7}$ | D. | $\frac{7}{12}$ |
9.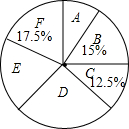 某学校将为初一学生开设ABCDEF共6门选修课,现选取若干学生进行了“我最喜欢的一门选修课”调查,将调查结果绘制成如图统计图表(不完整)
某学校将为初一学生开设ABCDEF共6门选修课,现选取若干学生进行了“我最喜欢的一门选修课”调查,将调查结果绘制成如图统计图表(不完整)
根据图表提供的信息,下列结论错误的是( )
 某学校将为初一学生开设ABCDEF共6门选修课,现选取若干学生进行了“我最喜欢的一门选修课”调查,将调查结果绘制成如图统计图表(不完整)
某学校将为初一学生开设ABCDEF共6门选修课,现选取若干学生进行了“我最喜欢的一门选修课”调查,将调查结果绘制成如图统计图表(不完整)| 选修课 | A | B | C | D | E | F |
| 人数 | 40 | 60 | 100 |
| A. | 这次被调查的学生人数为400人 | |
| B. | 扇形统计图中E部分扇形的圆心角为72° | |
| C. | 被调查的学生中喜欢选修课E、F的人数分别为80,70 | |
| D. | 喜欢选修课C的人数最少 |
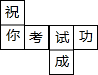 将“祝你考试成功”这六个字分别写在一个正方体的六个面上.若这个正方体的展开图如图所示,则在这个正方体中,与“你”字相对的字是( )
将“祝你考试成功”这六个字分别写在一个正方体的六个面上.若这个正方体的展开图如图所示,则在这个正方体中,与“你”字相对的字是( )