题目内容
18.小明在银行存入一笔零花钱.已知这种储蓄的年利率为n%,若设到期后的本息和(本金+利息)为y(元),存入的时间为x(年),那么,(1)下列哪个图象更能反映y与x之间的函数关系?从图中你能看出存入的本金是多少元?一年后的本息和是多少元?
(2)根据(1)的图象,求出y与x的函数关系式(不要求写出自变量x的取值范围),并求出两年后的本息和.

分析 (1)图1不能反映存入的本金,由图得出,存入的本金为0;图2既可反映存入的本金为100,也可得出存入1年后的本息和为102.25;图3不能反映存入的本金,可得出存入1年后的本息和为100;图4不能反映存入的本金,可得出存入1年后的本息和为102.25;
(2)由图2,根据待定系数法可将y与x之间的函数关系式表示出来,将x=2代入,可将两年后的本息和求出.
解答 解:(1)图2能反映y与x之间的函数关系,从图中可以看出存入的本金是100元
一年后的本息和是102.25元;
(2)设y与x的关系式为:y=nx+100,
把(1,102.25)代入上式得n=2.25,
∴y=2.25x+100,
当x=2时,y=2.25×2+100=104.5元,
所以两年后的本息和为104.5元.
点评 本题重点考查了一次函数的图象及一次函数的应用,要求学生从图象中将隐含的条件找出是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.下列结论中,不正确的是( )
| A. | 如果两条直线都和第三条直线平行,那么这两条直线也互相平行 | |
| B. | 如果两条直线都和第三条直线垂直,那么这两条直线也互相垂直 | |
| C. | 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行 | |
| D. | 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行 |
6.下列说法中正确的个数有( )
(1)在同一平面内,不相交的两条直线必平行;
(2)两条直线第三条直线所截,同旁内角互补;
(3)相等的角是对顶角;
(4)从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离;
(5)经过直线外一点,有且只有一条直线与已知直线平行.
(1)在同一平面内,不相交的两条直线必平行;
(2)两条直线第三条直线所截,同旁内角互补;
(3)相等的角是对顶角;
(4)从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离;
(5)经过直线外一点,有且只有一条直线与已知直线平行.
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
10.下列图象中,变量y不是变量x的函数的是( )
| A. |  | B. |  | C. |  | D. |  |
8.若x+y=5,则式子x2+2xy+y2+3的值为( )
| A. | 8 | B. | 13 | C. | 28 | D. | 64 |
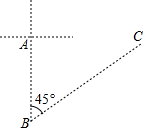 距沿海某城市A的正南方向300km的B处有一台风中心,根据海事预报,以台风中心为圆心,200km为半径的圆形区域内会受到台风影响.该台风中心现在正以18km\h的速度沿北偏东45°方向往C移动,问:该城市是否会受到这次台风的影响?请说明理由.($\sqrt{2}$≈1.4)
距沿海某城市A的正南方向300km的B处有一台风中心,根据海事预报,以台风中心为圆心,200km为半径的圆形区域内会受到台风影响.该台风中心现在正以18km\h的速度沿北偏东45°方向往C移动,问:该城市是否会受到这次台风的影响?请说明理由.($\sqrt{2}$≈1.4)