题目内容
10.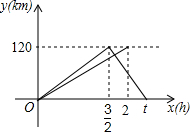 一辆轿车从甲地驶往乙地,到达乙地后立即返回甲地,速度是原来的1.5倍,往返共用t小时;一辆货车同时从甲地驶往乙地,到达乙地后停止,两车同时出发,匀速行驶,设轿车行驶的时间为x(h),两车离开甲地的距离为y(km),两车行驶过程中y与x之间的函数图象如图所示.
一辆轿车从甲地驶往乙地,到达乙地后立即返回甲地,速度是原来的1.5倍,往返共用t小时;一辆货车同时从甲地驶往乙地,到达乙地后停止,两车同时出发,匀速行驶,设轿车行驶的时间为x(h),两车离开甲地的距离为y(km),两车行驶过程中y与x之间的函数图象如图所示.(1)轿车从乙地返回甲地的速度为120km/h,t=$\frac{5}{2}$;
(2)求轿车从乙地返回甲地时y与x之间的函数关系式;
(3)当轿车从甲地返回乙地的途中与货车相遇时,求相遇处到甲地的距离.
分析 (1)根据图象可得当x=$\frac{3}{2}$小时时,据甲地的距离是120千米,即可求得轿车从甲地到乙地的速度,进而求得轿车从乙地返回甲地的速度和t的值;
(2)利用待定系数法即可求解;
(3)利用待定系数法求得轿车从乙地到甲地的函数解析式和货车路程和时间的函数解析式,求交点坐标即可.
解答 解:(1)轿车从甲地到乙地的速度是:$\frac{120}{\frac{3}{2}}$=80(千米/小时),
则轿车从乙地返回甲地的速度为80×1.5=120(千米/小时),
则t=$\frac{3}{2}$+$\frac{120}{120}$=$\frac{5}{2}$(小时).
故答案是:120,$\frac{5}{2}$;
(2)设y与x的函数解析式是y=kx+b,
则$\left\{\begin{array}{l}{\frac{3}{2}k+b=120}\\{\frac{5}{2}k+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-120}\\{b=300}\end{array}\right.$,
则函数解析式是y=-120x+300;
(3)设货车的解析式是y=mx,
则2m=120,
解得:m=60,
则函数解析式是y=60x.
根据题意得:$\left\{\begin{array}{l}{y=-120x+300}\\{y=60x}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=\frac{5}{3}}\\{y=100}\end{array}\right.$,
则轿车从甲地返回乙地的途中与货车相遇时,相遇处到甲地的距离是100千米.
点评 本题考查的是用一次函数解决实际问题,此类题是近年中考中的热点问题,正确解函数的解析式是关键.

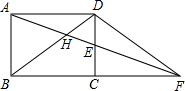 如图,矩形ABCD中,E为CD的中点,连接AE并延长交BC的延长线于点F,连接BD交AF于H,AD=10$\sqrt{2}$,且tan∠EFC=$\frac{\sqrt{2}}{4}$,那么AH的长为( )
如图,矩形ABCD中,E为CD的中点,连接AE并延长交BC的延长线于点F,连接BD交AF于H,AD=10$\sqrt{2}$,且tan∠EFC=$\frac{\sqrt{2}}{4}$,那么AH的长为( )| A. | $\frac{10\sqrt{6}}{3}$ | B. | 5$\sqrt{2}$ | C. | 10 | D. | 5 |
| A. | 6个只有颜色不同的小球 | |
| B. | 两个骰子 | |
| C. | 三个硬币 | |
| D. | 只有颜色不同的小卡片6张,其中红、白、黄各占2张 |
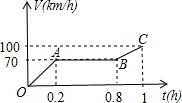 一辆摩托车从起点出发沿笔直的赛道向终点行驶,行驶中的速度V(km/h)与时间t(h)的关系部分信息如图所示,根据图象有下列说法:
一辆摩托车从起点出发沿笔直的赛道向终点行驶,行驶中的速度V(km/h)与时间t(h)的关系部分信息如图所示,根据图象有下列说法: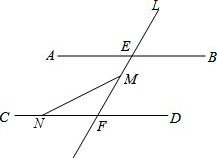 如图,AB∥CD,直L交AB、CD分别于点E、F,点M在线段EF上(点M不与E、F重合),N是直线CD上的一个动点(点N不与F重合)
如图,AB∥CD,直L交AB、CD分别于点E、F,点M在线段EF上(点M不与E、F重合),N是直线CD上的一个动点(点N不与F重合)