��Ŀ����
 ��ͼ����֪������y=x2+bx+c��ͼ����x���һ������ΪB��4��0������һ������ΪA������y�ύ�ڵ�C��0��4����
��ͼ����֪������y=x2+bx+c��ͼ����x���һ������ΪB��4��0������һ������ΪA������y�ύ�ڵ�C��0��4������1����ֱ��BC�������ߵĽ���ʽ��
��2������M����������ֱ��BC�·�ͼ���ϵ�һ���㣬����M��MH��y�ύֱ��BC�ڵ�N����MN�����ֵ��
��3���ڣ�2���������£�MNȡ�����ֵʱ������P����������ֱ��BC�·�ͼ���ϵ�һ�㣬�ҡ�ABP��������ABN�������ȣ�ֱ��д����P�����꣮
���㣺���κ����ۺ���
ר�⣺
��������1����ֱ��BC�Ľ���ʽΪy=mx+n����B��4��0����C��0��4�������������룬���ô���ϵ�����������ֱ��BC�Ľ���ʽ��ͬ������B��4��0����C��0��4��������������y=x2+bx+c�����ô���ϵ����������������ߵĽ���ʽ��
��2��MN�ij���ֱ��BC�ĺ���ֵ�������ߵĺ���ֵ�IJ�ݴ˿ɵó�һ������MN�ij���M�������ĺ�����ϵʽ�����ݺ��������ʼ������MN�����ֵ��
��3�������N������꣬���ݡ�ABP��������ABN�������ȣ����ǵĵ�AB��ͬ����Ӧ����ͬ�г����̣�Ȼ��ⷽ���飬���������P�����꣮
��2��MN�ij���ֱ��BC�ĺ���ֵ�������ߵĺ���ֵ�IJ�ݴ˿ɵó�һ������MN�ij���M�������ĺ�����ϵʽ�����ݺ��������ʼ������MN�����ֵ��
��3�������N������꣬���ݡ�ABP��������ABN�������ȣ����ǵĵ�AB��ͬ����Ӧ����ͬ�г����̣�Ȼ��ⷽ���飬���������P�����꣮
����⣺��1����ֱ��BC�Ľ���ʽΪy=mx+n��
��B��4��0����C��0��4���������������
��
���
��
����ֱ��BC�Ľ���ʽΪy=-x+4��
��B��4��0����C��0��4��������������y=x2+bx+c��
��
��
���
��
���������ߵĽ���ʽΪy=x2-5x+4��
��2����M��x��x2-5x+4����0��x��4������N��x��-x+4����
��MN=��-x+4��-��x2-5x+4��=-x2+4x=-��x-2��2+4��
�൱x=2ʱ��MN�����ֵ 4��
��3����MNȡ�����ֵʱ��x=2��
��-x+4=-2+4=2����N��2��2����
�ߡ�ABP��������ABN�������ȣ�
���ABP��AB���ϵĸߵ��ڡ�ABN��AB���ϵĸߣ�
��P����������2��-2��
��y=2����y=x2-5x+4��
��x1=
-
��x2=
+
���������⣬��ȥ����
��y=-2����y=x2-5x+4��
�ã�x3=2��x4=3��
�ʵ�P������ΪP1��
��2����P2��2��-2����P3 ��3��-2����
��B��4��0����C��0��4���������������
|
���
|
����ֱ��BC�Ľ���ʽΪy=-x+4��
��B��4��0����C��0��4��������������y=x2+bx+c��
��
|
���
|
���������ߵĽ���ʽΪy=x2-5x+4��
��2����M��x��x2-5x+4����0��x��4������N��x��-x+4����
��MN=��-x+4��-��x2-5x+4��=-x2+4x=-��x-2��2+4��
�൱x=2ʱ��MN�����ֵ 4��
��3����MNȡ�����ֵʱ��x=2��
��-x+4=-2+4=2����N��2��2����
�ߡ�ABP��������ABN�������ȣ�
���ABP��AB���ϵĸߵ��ڡ�ABN��AB���ϵĸߣ�
��P����������2��-2��
��y=2����y=x2-5x+4��
��x1=
| 5 |
| 2 |
| ||
| 2 |
| 5 |
| 2 |
| ||
| 2 |
��y=-2����y=x2-5x+4��
�ã�x3=2��x4=3��
�ʵ�P������ΪP1��
5-
| ||
| 2 |
�����������Ƕ��κ������ۺ��⣬�����漰�����ô���ϵ������һ�κ��������κ����Ľ���ʽ�����κ��������ʣ�����������������ͬ��һ���ȸߵ�֪ʶ�㣬�ۺ��Խ�ǿ������ѧ�����÷����顢���ν�ϵ�˼�뷽������2����Ū���߶�MN���ȵĺ��������ǹؼ�����3����ȷ��P���������ǹؼ���

��ϰ��ϵ�д�
 ֥�鿪���γ�������ϵ�д�
֥�鿪���γ�������ϵ�д� ����ѧ��ţ��Ӣ��ϵ�д�
����ѧ��ţ��Ӣ��ϵ�д�
�����Ŀ
����x����k��x-1��=4x-3k�ĸ���-4����k+8k��ֵ�ǣ�������
| A��-48 | B��0 | C��64 | D��72 |
 ��ͼ����AOB�У���B=30�㣬����AOB�Ƶ�O˳ʱ����ת52��õ���A��OB�䣬��A��B�����OB���ڵ�C��A�䲻��OB�ϣ������A��CO�Ķ�����
��ͼ����AOB�У���B=30�㣬����AOB�Ƶ�O˳ʱ����ת52��õ���A��OB�䣬��A��B�����OB���ڵ�C��A�䲻��OB�ϣ������A��CO�Ķ�����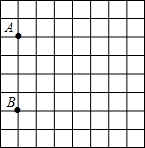 ��һ��ͼֽ��������������ͼ��������־��A��-3��1����B��-3��3�����ϣ�����Ҫ����C��3��2��������ͨ������ֱ������ϵ�ҵ�ͼ��C���λ�ã������ABC���ܳ���
��һ��ͼֽ��������������ͼ��������־��A��-3��1����B��-3��3�����ϣ�����Ҫ����C��3��2��������ͨ������ֱ������ϵ�ҵ�ͼ��C���λ�ã������ABC���ܳ��� ��ͼ��AE��BC����B=��C=50�㣬���DAC�Ķ�����
��ͼ��AE��BC����B=��C=50�㣬���DAC�Ķ����� ��ͼ��Բ�ڽ��ı���ABCD��AB�ǡ�O��ֱ����OD��BC��E��
��ͼ��Բ�ڽ��ı���ABCD��AB�ǡ�O��ֱ����OD��BC��E�� ��ͼ��AB=EB��BC=BF����ABE=��CBF����֤��EF=AC��
��ͼ��AB=EB��BC=BF����ABE=��CBF����֤��EF=AC��