题目内容
 如图,在菱形ABCD中,AD=13,BD=24,AC,BD交于点O.
如图,在菱形ABCD中,AD=13,BD=24,AC,BD交于点O.(1)求菱形ABCD的面积;
(2)求点O到边CD的距离.
考点:菱形的性质
专题:
分析:(1)利用菱形对角线互相垂直平分得出DO的长,再利用勾股定理得出AO的长,即可得出AC的长,再利用菱形面积求法得出;
(2)过点O作OE⊥CD于点E,利用(1)中所求得出OE的长即可.
(2)过点O作OE⊥CD于点E,利用(1)中所求得出OE的长即可.
解答:解:(1)∵四边形ABCD是菱形,
∴AC⊥BD,BO=DO,
∵AD=13,BD=24,
∴DO=12,
则AO=
=5,
故AC=10,
菱形ABCD的面积为:
×10×24=120;
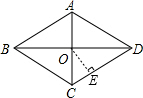 (2)过点O作OE⊥CD于点E,
(2)过点O作OE⊥CD于点E,
∵菱形ABCD的面积为:120,
∴S△COD=
×120=30,
∴
×EO×CD=30,
解得:EO=
.
∴AC⊥BD,BO=DO,
∵AD=13,BD=24,
∴DO=12,
则AO=
| 132-122 |
故AC=10,
菱形ABCD的面积为:
| 1 |
| 2 |
 (2)过点O作OE⊥CD于点E,
(2)过点O作OE⊥CD于点E,∵菱形ABCD的面积为:120,
∴S△COD=
| 1 |
| 4 |
∴
| 1 |
| 2 |
解得:EO=
| 60 |
| 13 |
点评:此题主要考查了菱形的性质以及勾股定理,得出DO的长是解题关键.

练习册系列答案
相关题目
二次函数y=-2(x-1)2+3的图象的顶点坐标是( )
| A、(1,3) |
| B、(-1,3) |
| C、(1,-3) |
| D、(-1,-3) |
关于x方程k(x-1)=4x-3k的根是-4,则k+8k的值是( )
| A、-48 | B、0 | C、64 | D、72 |
以下四个数中,比-1大的数是( )
| A、-π | ||
B、-
| ||
| C、-1 | ||
| D、0 |
 如图,已知:点B、D、C、F在一条直线上,且BD=FC,AB=EF,AB∥EF;△ABC≌△EFD吗?请说明理由.
如图,已知:点B、D、C、F在一条直线上,且BD=FC,AB=EF,AB∥EF;△ABC≌△EFD吗?请说明理由. 如图,△AOB中,∠B=30°,将△AOB绕点O顺时针旋转52°得到△A′OB′,边A′B′与边OB交于点C(A′不在OB上),求∠A′CO的度数.
如图,△AOB中,∠B=30°,将△AOB绕点O顺时针旋转52°得到△A′OB′,边A′B′与边OB交于点C(A′不在OB上),求∠A′CO的度数.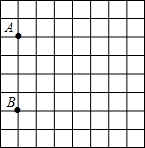 有一张图纸被损坏,但上面有如图的两个标志点A(-3,1),B(-3,3)可认,而主要建筑C(3,2)破损,请通过建立直角坐标系找到图中C点的位置,并求△ABC的周长.
有一张图纸被损坏,但上面有如图的两个标志点A(-3,1),B(-3,3)可认,而主要建筑C(3,2)破损,请通过建立直角坐标系找到图中C点的位置,并求△ABC的周长. 如图,AB=EB,BC=BF,∠ABE=∠CBF.求证:EF=AC.
如图,AB=EB,BC=BF,∠ABE=∠CBF.求证:EF=AC.